《2025年新课程课堂同步练习册七年级数学上册华师大版》

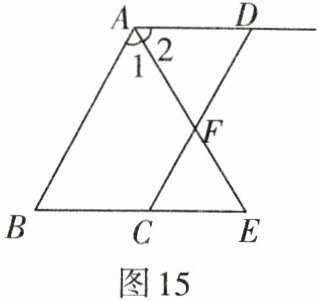
4. 如图15，$AB// CD$，$AE$平分∠$BAD$，$CD$与$AE$相交于$F$，∠$CFE$=∠$E$.
试说明：$AD// BC$.

答案： 4.
∵$AB// CD$
∴$\angle 1=\angle CFE$
∵$\angle CFE=\angle E$
∴$\angle 1=\angle E$
∵AE平分$\angle BAD$
∴$\angle 1=\angle 2$
∴$\angle 2=\angle E$
∴$AD// BE$即$AD// BC$

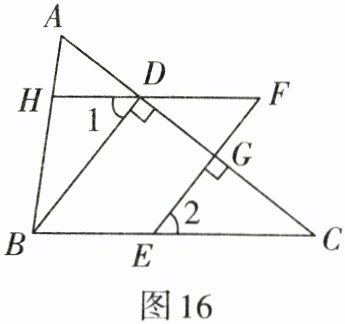
5. 如图16，$BD\perp AC$，垂足为点$D$，点$E$在$BC$上，$EF\perp AC$，垂足为点$G$，∠1=∠2.
(1)试说明：$DB// FE$；
(2)$HF$与$BC$的位置关系如何？ 为什么？
(3)若∠1=$x^{\circ}$，求∠$C$的度数(用含$x$的代数式表示).
注：本题第(1)、(2)小题在下面的解答过程的空格内填写理由或数学式；
第(3)小题要写出解题过程.
解：(1)∵$BD\perp AC$，$EF\perp AC$(已知)，
∴$DB// FE$().
(2)$HF$与$BC$的位置关系是：. 理由如下：
∵$DB// FE$，
∴∠1=∠()，
∵∠1=∠2(已知)，
∴∠2=∠()，
∴//().
(3)

答案： 1. （1）
解：
∵$BD\perp AC$，$EF\perp AC$（已知），
∴$DB// FE$（在同一平面内，垂直于同一条直线的两条直线互相平行）。
2. （2）
$HF$与$BC$的位置关系是：$HF// BC$。理由如下：
∵$DB// FE$，
∴$\angle1 = \angle F$（两直线平行，同位角相等），
∵$\angle1=\angle2$（已知），
∴$\angle2=\angle F$（等量代换），
∴$HF// BC$（内错角相等，两直线平行）。
3. （3）
解：因为$BD\perp AC$，所以$\angle BDC = 90^{\circ}$。
又因为$HF// BC$，所以$\angle HDC+\angle C = 180^{\circ}$（两直线平行，同旁内角互补）。
而$\angle HDC=\angle1 + \angle BDC$，已知$\angle1=x^{\circ}$，$\angle BDC = 90^{\circ}$，则$\angle HDC=(x + 90)^{\circ}$。
所以$(x + 90)+\angle C=180$，
移项可得$\angle C=180-(x + 90)$，
即$\angle C=(90 - x)^{\circ}$。
综上，答案依次为：（1）在同一平面内，垂直于同一条直线的两条直线互相平行；（2）$HF// BC$；$F$；两直线平行，同位角相等；$F$；等量代换；$HF$；$BC$；内错角相等，两直线平行；（3）$\angle C=(90 - x)^{\circ}$。