5. 如图6,OM,ON分别是$\angle BOC$和$\angle AOC$的平分线,且$\angle AOB = 84^{\circ}$.
(1)求$\angle MON$的度数;
(2)当OC在$\angle AOB$内转动时,$\angle MON$的值是否会变,简单说明理由.

(1)求$\angle MON$的度数;
(2)当OC在$\angle AOB$内转动时,$\angle MON$的值是否会变,简单说明理由.

答案:
5.
(1)$42^{\circ}$
(2)$\angle MON$的值不会变. 因为$\angle MON= \angle MOC+\angle CON=\frac{1}{2}\angle BOC+\frac{1}{2}\angle COA=\frac{1}{2}(\angle BOC+\angle COA)=\frac{1}{2}\angle AOB$
(1)$42^{\circ}$
(2)$\angle MON$的值不会变. 因为$\angle MON= \angle MOC+\angle CON=\frac{1}{2}\angle BOC+\frac{1}{2}\angle COA=\frac{1}{2}(\angle BOC+\angle COA)=\frac{1}{2}\angle AOB$
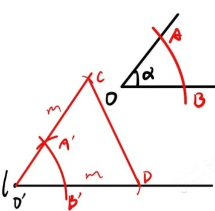
6. 如图7,已知一个等腰三角形的顶角等于$\angle\alpha$,腰长等于线段m,试利用尺规作图作出这个等腰三角形(不写作法,保留作图痕迹).


答案:

查看更多完整答案,请扫码查看


