2. 如图13,∠1=$30^{\circ}$,$AB\perp CD$,垂足为$O$,$EF$经过点$O$. 求∠2,∠3的度数.


答案:
2. $60^{\circ},30^{\circ}$
3. 如图14,在三角形$ABC$中,∠$BAC>90^{\circ}$.
(1)按下列要求画出相应的图形.
①过点$C$画直线$l// AB$;
②过点$A$分别画直线$BC$和直线$l$的垂线,
垂足分别为点$D$,$E$,$AE$交$BC$于点$F$.
(2)在所画出的图形中,按要求完成下列问题.
①线段
②在线段$AB$,$AD$,$AF$,$AC$中,长度最短的是线段
③延长$CA$至点$G$,试说明∠$BAG$=∠$B$+∠$ACB$.

(1)按下列要求画出相应的图形.
①过点$C$画直线$l// AB$;
②过点$A$分别画直线$BC$和直线$l$的垂线,
垂足分别为点$D$,$E$,$AE$交$BC$于点$F$.
(2)在所画出的图形中,按要求完成下列问题.
①线段
AD
的长度是点$A$到直线$BC$的距离,线段$AF$的长度是点F
到直线AB
的距离;②在线段$AB$,$AD$,$AF$,$AC$中,长度最短的是线段
AD
,理由是:直线外一点与直线上各点连接的所有线段中,垂线段
最短;③延长$CA$至点$G$,试说明∠$BAG$=∠$B$+∠$ACB$.

答案:
3.
(1)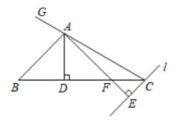
(2)①AD,F,AB ②AD,垂线段 ③
∵$CE// AB$
∴$\angle BCE=\angle B$,$\angle BAG=\angle ACE$
∵$\angle ACE=\angle BCE+\angle ACB$
∴$\angle BAG=\angle B+\angle ACB$
3.
(1)

(2)①AD,F,AB ②AD,垂线段 ③
∵$CE// AB$
∴$\angle BCE=\angle B$,$\angle BAG=\angle ACE$
∵$\angle ACE=\angle BCE+\angle ACB$
∴$\angle BAG=\angle B+\angle ACB$
查看更多完整答案,请扫码查看


