1. 先测量下面各图形的底和高,再分别计算出它们的面积。(精确到毫米。)
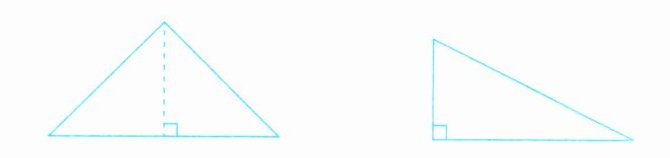
底(
高(
面积(

底(
2.2cm
) 底(2.0cm
)高(
1.1cm
) 高(1.0cm
)面积(
1.21cm²
) 面积(1cm²
)
答案:
1.先测量下面各图形的底和高,再分别计算出它们的面积。(精确到毫米。)


底(2.2cm) 底(2.0cm)
高(1.1cm) 高(1.0cm)
面积(1.21$cm^{2}$) 面积(1$cm^{2}$)
1.先测量下面各图形的底和高,再分别计算出它们的面积。(精确到毫米。)


底(2.2cm) 底(2.0cm)
高(1.1cm) 高(1.0cm)
面积(1.21$cm^{2}$) 面积(1$cm^{2}$)
(1) 两个完全一样的三角形可以拼成一个(
平行四边
)形,拼成的(平行四边
)形的底是原三角形的底,拼成的(平行四边
)形的高是原三角形的高,所以三角形的面积=(底
)×(高
)÷(2
)。
答案:
(1)两个完全一样的三角形可以拼成一个(平行四边)形,拼成的(平行四边)形的底是原三角形的底,拼成的(平行四边)形的高是原三角形的高,所以三角形的面积=(底)×(高)÷
(2)。
(1)两个完全一样的三角形可以拼成一个(平行四边)形,拼成的(平行四边)形的底是原三角形的底,拼成的(平行四边)形的高是原三角形的高,所以三角形的面积=(底)×(高)÷
(2)。
(2) 一个平行四边形的面积是$64m^{2}$,与它等底等高的三角形的面积是(
32
)$m^{2}$。
答案:
(2)一个平行四边形的面积是64$m^{2}$,与它等底等高的三角形的面积是
(32)$m^{2}$。
(2)一个平行四边形的面积是64$m^{2}$,与它等底等高的三角形的面积是
(32)$m^{2}$。
3. 一块平行四边形菜地的高是$26m$,底是高的3倍。这块菜地的面积是多少平方米?
答案:
3.一块平行四边形菜地的高是26m,底是高的3倍。这块菜地的面积是多少平方米?
26×3×26
=78×26
=2028($m^{2}$)
答:菜地面积是2028平方米。
26×3×26
=78×26
=2028($m^{2}$)
答:菜地面积是2028平方米。
4. 一块三角形的玻璃,它的底是$12dm$,高是$6.6dm$,每平方米玻璃的价钱是65元。买这块玻璃要用多少元?
答案:
4.一块三角形的玻璃,它的底是12dm,高是6.6dm,每平方米玻璃的价钱是65元。买这块玻璃要用多少元?
12×6.6÷2÷100×65=25.74(元)
答:要用25.74元。
12×6.6÷2÷100×65=25.74(元)
答:要用25.74元。
5. 有一个近似三角形的水池,底是$25.5m$,高是$12m$。这个水池占地面积有多大?

答案:
5.有一个近似三角形的水池,底是25.5m,高是12m。这个水池占地面积有多大?

25.5×12÷2
=306÷2
=153($m^{2}$)
答:水池占地面积153平方米。
5.有一个近似三角形的水池,底是25.5m,高是12m。这个水池占地面积有多大?

25.5×12÷2
=306÷2
=153($m^{2}$)
答:水池占地面积153平方米。
6. 把一个等边三角形分成4个面积相等的三角形。可以怎样分?你能想出几种方法?
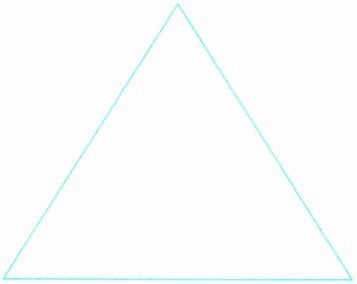

答案:
6.把一个等边三角形分成4个面积相等的三角形。可以怎样分?你能想出几种方法?



6.把一个等边三角形分成4个面积相等的三角形。可以怎样分?你能想出几种方法?



查看更多完整答案,请扫码查看


