《2025年能力培养与测试六年级数学上册人教版湖南专版》

1. 填一填。
(1)折一折,再填空。

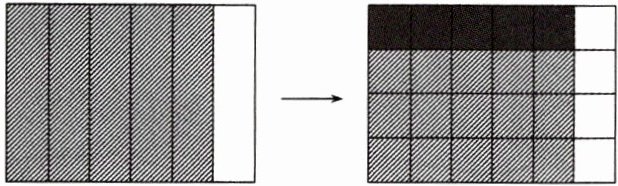
斜线部分的面积是这张纸面积的( ),黑色部分的面积是斜线部分面积的( ),黑色部分的面积是这张纸面积的多少,用算式表示是( )。
(2)计算$\frac{3}{8}×\frac{5}{6}$时,可以先把( )和( )进行约分,然后用分子( )×( )作为新的( ),分母( )×( )作为新的( )。
(3)在$◯$里填上“$＞$”“$＜$”或“$=$”。
$\frac{3}{4}×\frac{9}{5}◯\frac{3}{4}$ $\frac{5}{8}×\frac{7}{3}◯\frac{5}{8}$
$\frac{7}{12}×\frac{6}{7}◯\frac{3}{4}×\frac{2}{3}$ $0×\frac{7}{10}◯\frac{7}{10}$
(4)已知甲数是$\frac{8}{15}$,乙数是甲数的$\frac{1}{2}$,则乙数是( )。
(5)$\frac{6}{7}t的\frac{13}{12}$是( )t。

答案： （1）$\frac{5}{6}$ $\frac{1}{4}$ $\frac{5}{6}×\frac{1}{4}=\frac{5}{24}$ （2）3 6 1 5 分子 8 2 分母 （3）＞ ＞ = ＜ （4）$\frac{4}{15}$ （5）$\frac{13}{14}$

2. 看谁算得又快又准。
$\frac{1}{2}×\frac{5}{7}= $ $\frac{4}{9}×\frac{3}{5}= $ $0×\frac{5}{4}= $
$\frac{5}{12}×\frac{9}{25}= $ $\frac{8}{35}×\frac{21}{10}= $ $\frac{10}{21}×\frac{7}{15}= $

答案： $\frac{5}{14}$ $\frac{4}{15}$ 0 $\frac{3}{20}$ $\frac{12}{25}$ $\frac{2}{9}$

3. 大豆是含蛋白质最多的豆类。$1kg大豆约含\frac{2}{5}kg$蛋白质,$\frac{3}{4}kg$大豆约含蛋白质多少千克？

答案： $\frac{2}{5}×\frac{3}{4}=\frac{3}{10}$（kg）

4. 路边有一块长方形绿化带,绿化带的宽是$\frac{9}{10}m$,长是宽的$5$倍,长是多少米？这块绿化带的面积是多少平方米？

答案： 绿化带长：$\frac{9}{10}×5=\frac{9}{2}$（m） 绿化带面积：$\frac{9}{10}×\frac{9}{2}=\frac{81}{20}$（m²）

5. (1)先观察下面算式有什么规律,再填写。
$\frac{1}{2}×\frac{1}{3}= \frac{1}{2×3}= \frac{1}{2}-\frac{1}{3}$,
$\frac{1}{3}×\frac{1}{4}= \frac{1}{3×4}= \frac{1}{3}-\frac{1}{4}$,
$\frac{1}{4}×\frac{1}{5}= \frac{1}{4×5}= \frac{1}{4}-\frac{1}{5}$,
$\frac{1}{6}×\frac{1}{7}= $ ,
$\frac{1}{9}×\frac{1}{10}= $ 。
(2)根据规律计算：
$\frac{1}{7}×\frac{1}{8}+\frac{1}{8}×\frac{1}{9}+\frac{1}{9}×\frac{1}{10}$。

答案： （1）$\frac{1}{6}-\frac{1}{7}$ $\frac{1}{9}-\frac{1}{10}$ （2）$\frac{3}{70}$