搜索
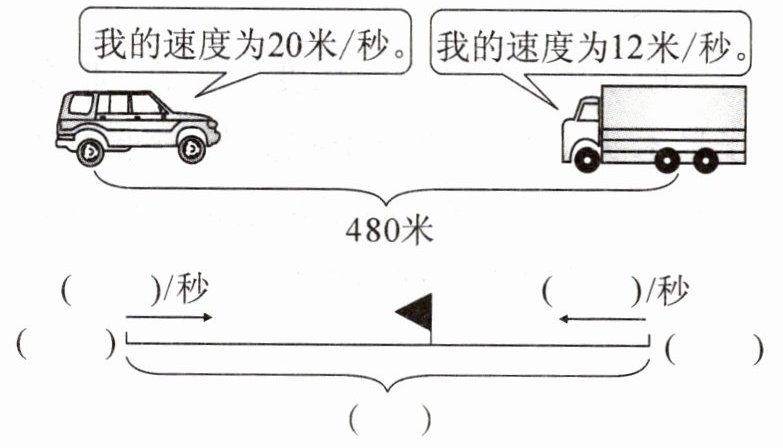
2. 先根据题意完成线段图,再列方程解答。
吉普车和货车同时出发,$x$秒两车相遇。
( )/秒
( )/秒
( )
( )
( )
吉普车和货车同时出发,$x$秒两车相遇。
( )/秒
( )/秒
( )
( )
( )
答案：
2. 20米 12米 吉普车 货车 480米 20x+12x=480 x=15
3. 大客车和小轿车同时从相距$413$km的甲、乙两地相对开出,经过几小时后两车相遇？
答案：
3. 解:设经过x小时后两车相遇。56x+62x=413 x=3.5 答:经过3.5小时后两车相遇。
4. 甲、乙两艘轮船从相距$350$km的 A,B两港同时出发,相向行驶,$5$小时后相遇。甲船每小时行$32.5$km,乙船每小时行多少千米？
答案：
4. 解:设乙船每小时行x km。(32.5+x)×5=350 x=37.5 答:乙船每小时行37.5 km。
5. 小红和小明同时从相距$3$km的甲、乙两地面对面比赛跑步,小红到达乙地后立即返回继续跑,小明到达甲地后也立即返回继续跑,从开始跑到两人第二次相遇用了$24$分钟。已知小红每分钟跑$200$m,求小明每分钟跑多少米。
答案：
5. 解析:如图所示。
到第二次相遇两人共跑了3个3 km，再根据“速度×时间=路程”列出方程。解:设小明每分钟跑x m。200×24+24x=3×3000 x=175 答:小明每分钟跑175 m。
5. 解析:如图所示。
到第二次相遇两人共跑了3个3 km，再根据“速度×时间=路程”列出方程。解:设小明每分钟跑x m。200×24+24x=3×3000 x=175 答:小明每分钟跑175 m。 1. 填一填。
(1)长方形的面积公式用字母表示是( ),若$a = 6\mathrm{cm}$,$b = 4.3\mathrm{cm}$,则长方形的面积是( )$\mathrm{cm}^2$。
(2)解方程$(40 - 2x)÷ 4 = 2$时,先把( )看作一个整体,再把( )看作一个整体。
(3)在$(40 - 2x)÷ 4$中,当$x = ( )时,结果是$0$；当$x = ( )时,结果是$1$。
(4)学校有足球$x$个,排球的个数比足球的$2倍少3$个,学校有足球和排球共( )个。
(1)长方形的面积公式用字母表示是( ),若$a = 6\mathrm{cm}$,$b = 4.3\mathrm{cm}$,则长方形的面积是( )$\mathrm{cm}^2$。
(2)解方程$(40 - 2x)÷ 4 = 2$时,先把( )看作一个整体,再把( )看作一个整体。
(3)在$(40 - 2x)÷ 4$中,当$x = ( )时,结果是$0$；当$x = ( )时,结果是$1$。
(4)学校有足球$x$个,排球的个数比足球的$2倍少3$个,学校有足球和排球共( )个。
答案：
1.（1）S=ab 25.8 （2）40-2x 2x （3）20 18 （4）3x-3
2. 判断。(正确的画“√”,错误的画“×”)
(1)$5a + 8b = 13ab$。( )
(2)$7 + 8 = 9 + 6$是等式,不是方程。( )
(3)方程的解不可能是$0$。( )
(4)方程$4x + 9 = 45的解是x = 9$。( )
(1)$5a + 8b = 13ab$。( )
(2)$7 + 8 = 9 + 6$是等式,不是方程。( )
(3)方程的解不可能是$0$。( )
(4)方程$4x + 9 = 45的解是x = 9$。( )
答案：
2.（1）× （2）√ （3）× （4）√
查看更多完整答案，请扫码查看
