第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
5. 下面各组算式中,得数不相同的是(
A.$\begin{cases}125×8 + 0\\125×0×8\end{cases} $
B.$\begin{cases}25×17×4\\25×4×17\end{cases} $
C.$\begin{cases}25×14\\25×(10 + 4)\end{cases} $
D.$\begin{cases}34×101\\34×100 + 34\end{cases} $
A
)。A.$\begin{cases}125×8 + 0\\125×0×8\end{cases} $
B.$\begin{cases}25×17×4\\25×4×17\end{cases} $
C.$\begin{cases}25×14\\25×(10 + 4)\end{cases} $
D.$\begin{cases}34×101\\34×100 + 34\end{cases} $
答案:
A
6. 下图是两名同学计算 $125×72$ 的过程,他们分别用到了(

①乘法分配律 ②乘法交换律 ③乘法结合律 ④加法交换律
A.③①
B.②③
C.①②
D.③④
A
)。
①乘法分配律 ②乘法交换律 ③乘法结合律 ④加法交换律
A.③①
B.②③
C.①②
D.③④
答案:
A
7. 下面的算式去掉括号后,得到的算式结果与原算式相等的是(
A.$45×(26×3) - 74$
B.$45×(26 + 3) - 74$
C.$45×(26 - 3) - 74$
D.$45×(26 - 3)×74$
A
)。A.$45×(26×3) - 74$
B.$45×(26 + 3) - 74$
C.$45×(26 - 3) - 74$
D.$45×(26 - 3)×74$
答案:
A
8. 某工厂加工了一批长方形贴纸(如下面左图所示),下面方框中(
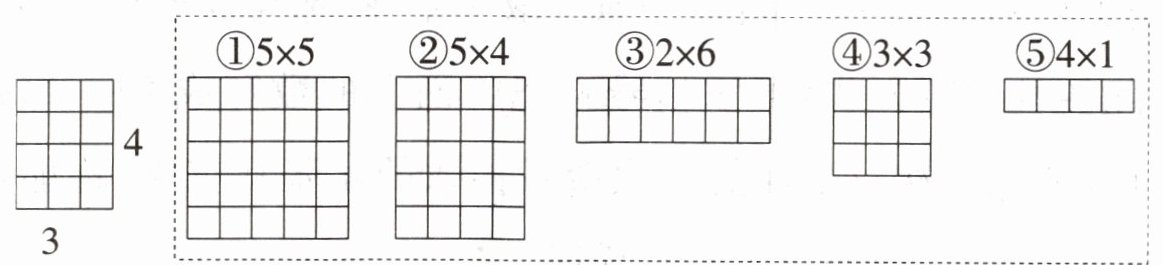
A.②③④
B.②③⑤
C.②④⑤
D.①②③
C
)贴纸能和左图的贴纸拼成一张更大的长方形贴纸。
A.②③④
B.②③⑤
C.②④⑤
D.①②③
答案:
C
9. 杨杨最近学习了运算律,他发现运用运算律有时可以让计算变得更加简单。在计算一道三位数乘两位数的算式时,他惊奇地发现竖式计算中也蕴含着运算律。
(1) 请你将括号里的内容补充完整,并结合竖式想一想,该竖式计算中运用了哪种运算律?说明你的理由。
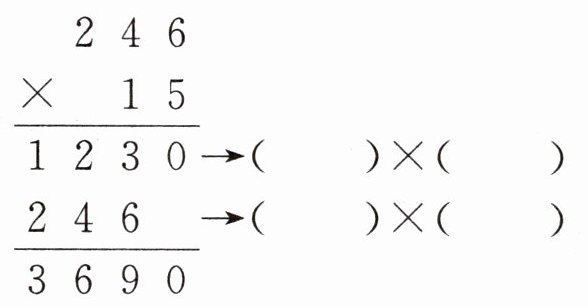
(2) 请你再举一个例子,说明怎样运用以上运算律计算三位数乘两位数的算式。
(1)246×15的竖式计算中,把15拆成10和5,246×15 = 246×(10 + 5)=246×10 + 246×5,运用了乘法分配律。
(2)答案不唯一,举例合理即可。
(1) 请你将括号里的内容补充完整,并结合竖式想一想,该竖式计算中运用了哪种运算律?说明你的理由。
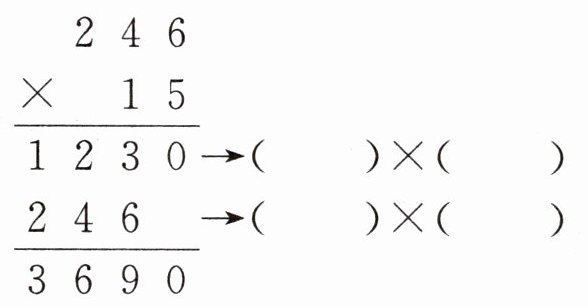
(2) 请你再举一个例子,说明怎样运用以上运算律计算三位数乘两位数的算式。
(1)246×15的竖式计算中,把15拆成10和5,246×15 = 246×(10 + 5)=246×10 + 246×5,运用了乘法分配律。
(2)答案不唯一,举例合理即可。
答案:
(1)246×15的竖式计算中,把15拆成10和5,246×15 = 246×(10 + 5)=246×10 + 246×5,运用了乘法分配律。
(2)答案不唯一,举例合理即可。
(1)246×15的竖式计算中,把15拆成10和5,246×15 = 246×(10 + 5)=246×10 + 246×5,运用了乘法分配律。
(2)答案不唯一,举例合理即可。
查看更多完整答案,请扫码查看


