第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 填一填,画一画。
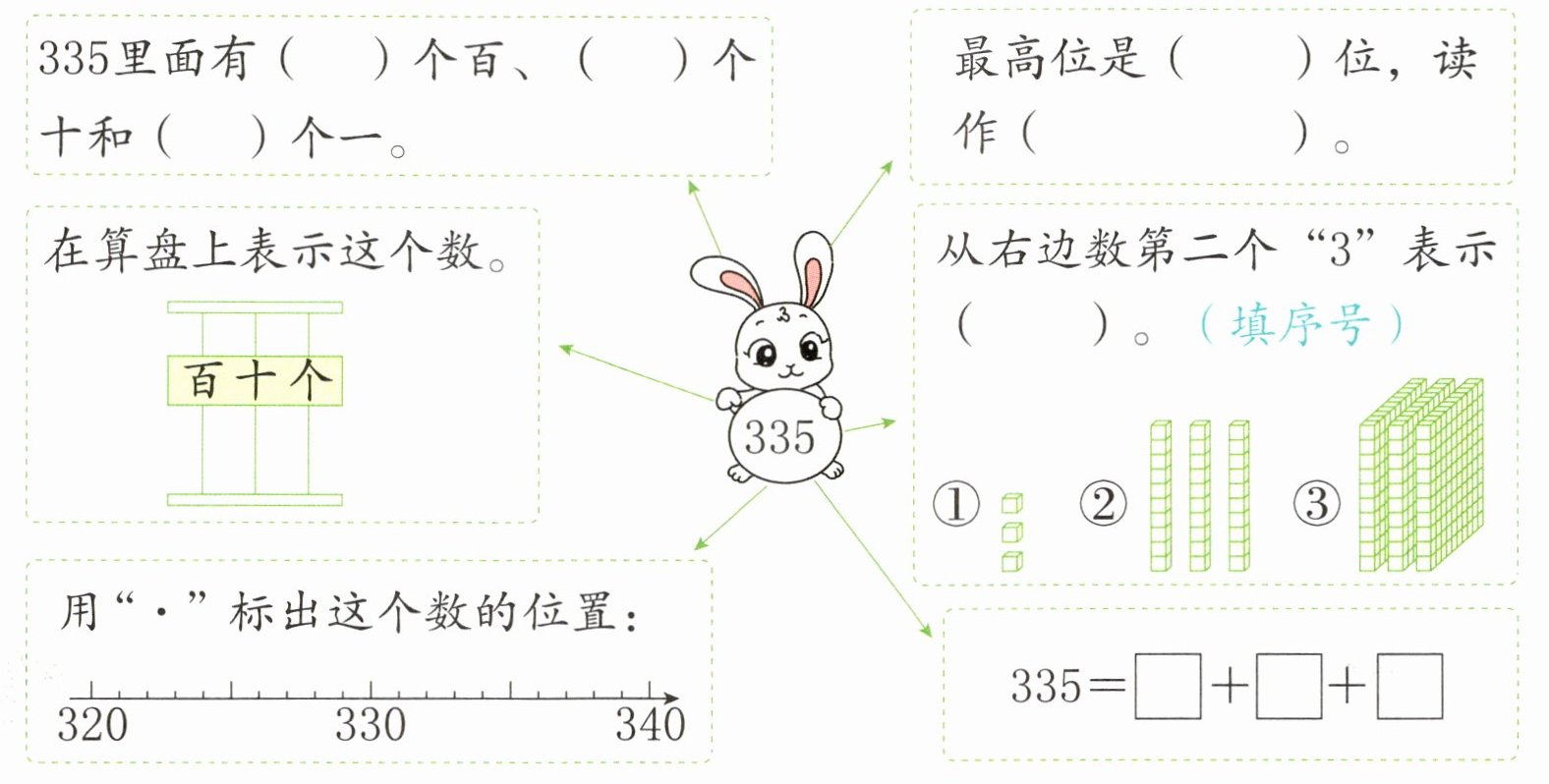
335里面有( )个百、( )个十和( )个一。
最高位是( )位,读作( )。
在算盘上表示这个数。
百十个
用“·”标出这个数的位置:
320 330 340
从右边数第二个“3”表示( )。(填序号)
① ② ③
335= □+□+□

335里面有( )个百、( )个十和( )个一。
最高位是( )位,读作( )。
在算盘上表示这个数。
百十个
用“·”标出这个数的位置:
320 330 340
从右边数第二个“3”表示( )。(填序号)
① ② ③
335= □+□+□
答案:
3 3 5 百 三百三十五 ③ 300 30 5
百 三百三十五 ③ 300 30 5
3 3 5
 百 三百三十五 ③ 300 30 5
百 三百三十五 ③ 300 30 5 2. 在○里填上“>”“<”或“=”。
990○980 750-50○700 500+80+5○590
789○800 400+90○560-60 800+60+7○900+7
990○980 750-50○700 500+80+5○590
789○800 400+90○560-60 800+60+7○900+7
答案:
> = < < < <
3. 估一估,填一填。(教材P73第7题变式)
(1)大约有多少本?
( )本 ( )本 100本
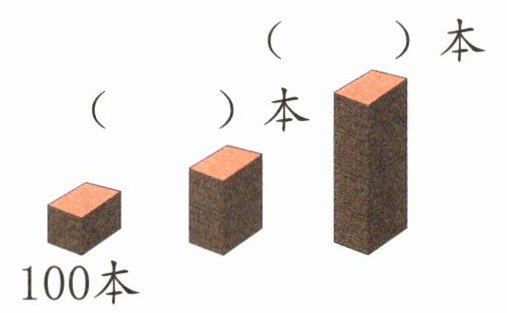
(2)大约再放入( )颗能装满。
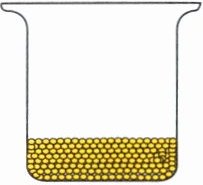
大约300颗。
(1)大约有多少本?
( )本 ( )本 100本

(2)大约再放入( )颗能装满。

大约300颗。
答案:
(1)200 400 (合理即可)
(2)900 (合理即可)
(1)200 400 (合理即可)
(2)900 (合理即可)
4. 拨一拨,填一填。
(1)如图,文文在算盘上拨出的数是( ),如果文文再拨一个算珠靠梁,表示的三位数可能是( )。
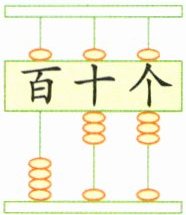
(2)诺诺在算盘上用1个上珠和2个下珠表示数,一共可以表示出( )个不同的三位数。
(1)如图,文文在算盘上拨出的数是( ),如果文文再拨一个算珠靠梁,表示的三位数可能是( )。

(2)诺诺在算盘上用1个上珠和2个下珠表示数,一共可以表示出( )个不同的三位数。
答案:
(1)588 688、598 或 589
(2)12 【解析】用 1 个上珠和 2 个下珠表示三位数,可以分成四种情况进行讨论。第一种情况:个位、十位和百位上均有一个珠子。可以组成 151、115、511 三个三位数。第二种情况:一个上珠和一个下珠在同一个数位上。可以组成 106、160、601、610 四个三位数。第三种情况:两个下珠在同一个数位上。可以组成 502、520、205、250 四个三位数。第四种情况:三个珠子在同一个数位上,可以组成 700 一个三位数,则一共可以组成 3+4+4+1=12(个)不同的三位数。
(1)588 688、598 或 589
(2)12 【解析】用 1 个上珠和 2 个下珠表示三位数,可以分成四种情况进行讨论。第一种情况:个位、十位和百位上均有一个珠子。可以组成 151、115、511 三个三位数。第二种情况:一个上珠和一个下珠在同一个数位上。可以组成 106、160、601、610 四个三位数。第三种情况:两个下珠在同一个数位上。可以组成 502、520、205、250 四个三位数。第四种情况:三个珠子在同一个数位上,可以组成 700 一个三位数,则一共可以组成 3+4+4+1=12(个)不同的三位数。
查看更多完整答案,请扫码查看


