《2025年衡水名师新作高一物理》

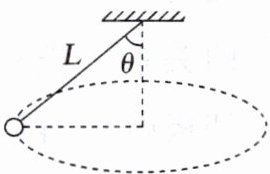
6. (多选)(2025·山东省泰安市高一期末)如图所示,轻绳拉着质量 $ m = 1 \text{ kg} $ 的小球在光滑水平面上做圆周运动,轻绳长 $ L = 1.5 \text{ m} $,轻绳与竖直方向的夹角 $ \theta = 53^\circ $,取 $ g = 10 \text{ m/s}^2 $,$ \sin 53^\circ = 0.8 $,$ \cos 53^\circ = 0.6 $。当小球角速度增大为 $ \omega = \frac{\sqrt{40}}{3} \text{ rad/s} $ 时(BD)

A.光滑水平面对小球支持力大小为 $ 9 \text{ N} $
B.光滑水平面对小球支持力为零
C.轻绳拉力的大小为 $ 10 \text{ N} $
D.轻绳拉力的大小为 $ 20 \text{ N} $

答案： BD[对小球受力分析,由牛顿第二定律得:水平方向:$F \sin \theta = m \omega ^ { 2 } L \sin \theta$,代入数据得:$F = 20 N$,由于:$F \cos \theta = 20 × 0.8 N = 16 N ＞ 10 N = m g$,所以球对水平面无挤压,支持力为零,故AC错误,BD正确。]

7. (2025·江苏省常州市期中)如图所示为脚踏自行车的传动装置简化图,甲、乙两轮同轴且无相对转动,传动链条在各轮转动中不打滑,$ A $、$ B $、$ C $ 分别是甲、乙、丙三轮边缘上的点,则(D)

A.周期 $ T_A ＞ T_B $
B.线速度 $ v_A = v_B $
C.角速度 $ \omega_A ＜ \omega_C $
D.向心加速度 $ a_B ＞ a_C $

答案： D[C.甲和丙链条转动,所以其线速度大小相等,即$v _ { A } = v _ { C }$,根据线速度与角速度的关系$v = \omega r$,因为$r _ { A } ＜ r _ { C }$,所以$\omega _ { A } ＞ \omega _ { C }$,甲和乙同轴转动,则二者角速度相等,即$\omega _ { A } = \omega _ { B }$,则有$\omega _ { A } = \omega _ { B } ＞ \omega _ { C }$,故C错误;A.根据周期和角速度的关系$T = \frac { 2 \pi } { \omega }$可得周期$T _ { A } = T _ { B }$,故A错误;B.根据线速度与角速度的关系$v = \omega r$且$r _ { A } ＜ r _ { B }$可得线速度$v _ { A } ＜ v _ { B }$,故B错误;D.对甲、丙由向心加速度表达式有$a = \frac { v ^ { 2 } } { r }$,根据$v _ { A } ＜ v _ { B }$,$r _ { A } ＜ r _ { C }$,可得$a _ { A } ＞ a _ { C }$,对甲、乙$a = \omega ^ { 2 } r$由根据$\omega _ { A } = \omega _ { B }$,$r _ { A } ＜ r _ { B }$,可得$a _ { A } ＜ a _ { B }$,故$a _ { C } ＜ a _ { A } ＜ a _ { B }$,故D正确。]

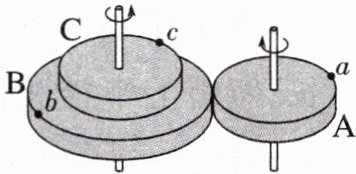
8. (2025·河南省安阳市高一期末)如图所示,$ B $ 和 $ C $ 是一组塔轮,$ B $ 和 $ C $ 半径不同,但固定在同一转轴上,其半径之比为 $ R_B:R_C = 3:2 $,$ A $ 轮的半径大小与 $ C $ 轮相同,它与 $ B $ 轮紧靠在一起,当 $ A $ 轮绕过其中心的竖直轴转动时,由于摩擦力作用,$ B $ 轮也随之无滑动地转动起来。$ a $、$ b $、$ c $ 分别为三轮边缘上的三个点,则 $ a $、$ b $、$ c $ 三点在运动过程中的(D)

A.线速度大小之比为 $ 3:2:2 $
B.角速度之比为 $ 3:3:2 $
C.转速之比为 $ 2:3:2 $
D.向心加速度大小之比为 $ 9:6:4 $

答案： D[$A、B$靠摩擦传动,则两轮边缘上$a、b$两点的线速度大小相等,即$v _ { a } : v _ { b } = 1 : 1$,选项A错误;$B、C$同轴转动,则两轮边缘上$b、c$两点的角速度相等,即$\omega _ { b } = \omega _ { c }$,转速之比$\frac { n _ { b } } { n _ { c } } = \frac { \omega _ { b } } { \omega _ { c } } = \frac { 1 } { 1 }$,选项B、C错误;对$a、b$两点,由$a _ { n } = \frac { v ^ { 2 } } { r }$得$\frac { a _ { a } } { a _ { b } } = \frac { R _ { B } } { R _ { A } } = \frac { 3 } { 2 }$,对$b、c$两点,由$a _ { n } = \omega ^ { 2 } r$得$\frac { a _ { b } } { a _ { c } } = \frac { R _ { B } } { R _ { C } } = \frac { 3 } { 2 }$,故$a _ { a } : a _ { b } : a _ { c } = 9 : 6 : 4$,选项D正确。]

(多选)(2025·四川省成都市温江区校级月考)如图所示,用一根长杆和两个定滑轮的组合装置来提升重物 $ M $,长杆的一端放在地面上通过铰链连结形成转轴,其端点恰好处于左侧滑轮正下方 $ O $ 点处,在杆的中点 $ C $ 处拴一细绳,通过两个滑轮后挂上重物 $ M $,$ C $ 点与 $ O $ 点距离为 $ L $,现在杆的另一端用力,使其逆时针匀速转动,由竖直位置以角速度 $ \omega $ 缓缓转至水平(转过了 $ 90^\circ $ 角)。下列有关此过程的说法正确的是BD
A.重物 $ M $ 做匀速直线运动
B.重物 $ M $ 做变速直线运动
C.重物 $ M $ 的最大速度是 $ 2\omega L $
D.重物 $ M $ 的速度先增大后减小

答案： BD[设C点线速度方向与绳子沿线的夹角为θ(锐角),由题知C点的线速度为$\omega L$,该线速度在绳子方向上的分速度为$\omega L \cos \theta$。θ的变化规律是开始最大($90 ^ { \circ }$),然后逐渐变小,所以$\omega L \cos \theta$逐渐变大,直至绳子和杆垂直,θ变为$0 ^ { \circ }$,绳子的速度变为最大,为$\omega L$;然后,θ又逐渐增大,$\omega L \cos \theta$逐渐变小,绳子的速度变慢。所以知重物的速度先增大后减小,最大速度为$\omega L$。故B、D正确,A、C错误。]