《2025年衡水名师新作高一物理》

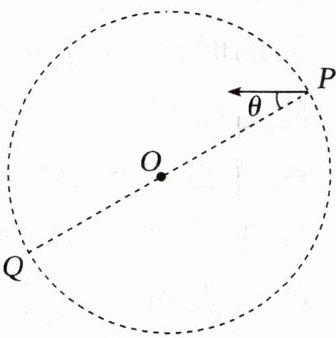
(2025·安徽省合肥六中高一期末)如图所示,竖直面内有一以O为圆心的圆形区域,圆的半径R = 20m,直径PQ与水平方向间的夹角θ = 30°。小球自P点水平射入圆形区域,不计空气阻力,g取$10m/s^2。$
(1)若使小球从Q点射出,求其在圆形区域中运动时间t;
(2)若使小球从Q点射出,求其到达Q点时的速度大小;
(3)为使小球在圆形区域运动时间最长,求该小球进入圆形区域时的速度v大小。(以上计算结果均可保留根式)

答案：
[解析]
(1)小球做平抛运动,小球从Q点射出时如图所示:竖直方向:$ h_1 = 2R \sin \theta = \frac{1}{2} g t^2 $，代入数据解得:$ t = 2 s $;
(2)小球从Q点射出,水平方向:$ x_1 = 2R \cos \theta = v_0 t $
到达Q点时的竖直分速度 $ v_y = g t $
到达Q点时的速度大小 $ v_Q = \sqrt{v_0^2 + v_y^2} $
代入数据解得:$ v_Q = 10 \sqrt{7} m/s $;
(3)平抛运动的运动时间由竖直方向的分运动决定,当竖直分位移最大时小球的运动时间最长,当小球从圆形区域的最低点射出时运动时间最长,在竖直方向:$ h_2 = R + R \sin \theta = \frac{1}{2} g t'^2 $，水平方向:$ x_2 = R \cos \theta = v t' $
代入数据解得:$ v = 5 \sqrt{2} m/s $
$[答案] (1)2s (2)10\sqrt{7}m/s (3)5\sqrt{2}m/s$

(1)关于该实验应注意的问题,下列做法合理的是AD;
(2)在该实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,同学甲和同学乙得到的记录纸如图2所示,从图中明显看出甲的实验错误是斜槽末端不水平,乙图中有两个点位于抛物线下方的原因是静止释放小球的位置不同;
(3)丙同学不小心将记录实验的坐标纸弄破损,导致平抛运动的初始位置缺失。他选取轨迹上的某一点做为坐标原点O,建立xOy坐标系(x轴沿水平方向,y轴沿竖直方向),如图3所示。在轨迹上选取A、B两点,坐标纸中每个小方格的边长为L,重力加速度为g,根据题中所给信息,可以求出小球从O点运动到A点所用的时间t = $\sqrt{\frac{2L}{g}}$,小球平抛运动的初速度v₀ = $2 \sqrt{2gL}$(计算结果用L,g表示)

答案： [解析]
(1)关于该实验应注意的问题,下列做法合理的是______;
A.应使小球每次从斜槽上同一位置由静止释放
B.调节挡板的高度时必须等间距变化
C.建立坐标系时,坐标原点应为斜槽口的末端
D.小球运动时不应与木板上的白纸(或方格纸)相接触
(2)在该实验中,让小球多次从斜槽上滚下,在白纸上依次记下小球的位置,同学甲和同学乙得到的记录纸如图2所示,从图中明显看出甲的实验错误是______,乙图中有两个点位于抛物线下方的原因是______;
(3)丙同学不小心将记录实验的坐标纸弄破损,导致平抛运动的初始位置缺失。他选取轨迹上的某一点做为坐标原点O,建立xOy坐标系(x轴沿水平方向,y轴沿竖直方向),如图3所示。在轨迹上选取A、B两点,坐标纸中每个小方格的边长为L,重力加速度为g,根据题中所给信息,可以求出小球从O点运动到A点所用的时间t = ______,小球平抛运动的初速度v₀ = ______(计算结果用L,g表示)
探究提示:
(1)A.为了保证小球每次抛出的速度相同,应使小球每次从斜槽上同一位置由静止释放,故A正确;B.调节挡板的高度时不需要等间距变化,故B错误;C.建立坐标系时,坐标原点应为小球处于斜槽口末端时球心在白纸上的水平投影点,故C错误;D.为了减小误差,小球运动时不应与木板上的白纸(或方格纸)相接触,故D正确;
(2)从图2中明显看出甲的实验错误是:小球抛出时的速度不是水平方向,即斜槽末端不水平;乙图中有两个点位于抛物线下方的原因是静止释放小球的位置不同;
(3)竖直方向根据:$ \Delta y = y_{AB} - y_{OA} = 5L - 3L = g t^2 $
可得小球从O点运动到A点所用的时间为:$ t = \sqrt{\frac{2L}{g}} $
水平方向根据:$ x = 4L = v_0 t $
可得小球平抛运动的初速度为:$ v_0 = 2 \sqrt{2gL} $
[答案]
(1)AD
(2)斜槽末端不水平 静止释放小球的位置不同
(3)$ \sqrt{\frac{2L}{g}} $ $ 2 \sqrt{2gL} $