《2025年衡水名师新作高一物理》

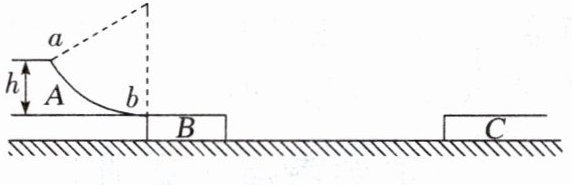
(2024·海南卷,17)某游乐项目装置简化如图,A为固定在地面上的光滑圆弧形滑梯,半径$R= 10m$,滑梯顶点a与滑梯末端b的高度$h= 5m$,静止在光滑水平面上的滑板B,紧靠滑梯的末端,并与其水平相切,滑板质量$M= 25kg$,一质量为$m= 50kg$的游客,从a点由静止开始下滑,在b点滑上滑板,当滑板右端运动到与其上表面等高平台的边缘时,游客恰好滑上平台,并在平台上滑行$s= 16m$停下。游客视为质点,其与滑板及平台表面之间的动摩擦因数均为$\mu =0.2$,忽略空气阻力,重力加速度$g= 10m/s^{2}$,求:
(1)游客滑到b点时对滑梯的压力的大小;
(2)滑板的长度L。

答案：
(1)设游客滑到$b$点时速度为$v_{0}$，从$a$到$b$过程，根据机械能守恒定律：
$mgh = \frac{1}{2}mv_{0}^{2}$
代入数据解得：
$v_{0} = \sqrt{2gh} = \sqrt{2×10×5} = 10\,\text{m/s}$
在$b$点，根据牛顿第二定律：
$F_{N} - mg = m\frac{v_{0}^{2}}{R}$
代入数据解得：
$F_{N} = mg + m\frac{v_{0}^{2}}{R} = 50×10 + 50×\frac{10^{2}}{10} = 1000\,\text{N}$
根据牛顿第三定律，游客对滑梯的压力大小为：
$F_{N}' = F_{N} = 1000\,\text{N}$
(2)设游客滑上平台时的速度为$v$，在平台上滑行过程，由动能定理：
$-\mu mgs = 0 - \frac{1}{2}mv^{2}$
代入数据解得：
$v = \sqrt{2\mu gs} = \sqrt{2×0.2×10×16} = 8\,\text{m/s}$
游客在滑板上滑行时，加速度大小：
$a_{1} = \mu g = 0.2×10 = 2\,\text{m/s}^{2}$
滑板的加速度大小：
$a_{2} = \frac{\mu mg}{M} = \frac{0.2×50×10}{25} = 4\,\text{m/s}^{2}$
设滑行时间为$t$，对游客：
$v = v_{0} - a_{1}t$
代入数据解得：
$t = \frac{v_{0} - v}{a_{1}} = \frac{10 - 8}{2} = 1\,\text{s}$
游客的位移：
$s_{1} = \frac{v_{0} + v}{2}t = \frac{10 + 8}{2}×1 = 9\,\text{m}$
滑板的位移：
$s_{2} = \frac{1}{2}a_{2}t^{2} = \frac{1}{2}×4×1^{2} = 2\,\text{m}$
滑板长度：
$L = s_{1} - s_{2} = 9 - 2 = 7\,\text{m}$
(1)$1000\,\text{N}$
(2)$7\,\text{m}$

(1)图乙中图线斜率$k= $$-2$;
(2)传感器示数$F_{0}= $$4.9$N;
(3)若某次该钢球由静止释放时细线与竖直方向的夹角为θ、在最低点时传感器示数$F_{2}= 7.35N$,则$cosθ= $$\frac{3}{4}$。

答案：
(1)
钢球静止于最低点时，由平衡条件得：$F_{0}=mg$。
释放点时，沿绳方向合力为零，有：$F_{1}=mg\cos\theta$。
下摆至最低点过程机械能守恒：$mgL(1-\cos\theta)=\frac{1}{2}mv^{2}$。
最低点由牛顿第二定律：$F_{2}-mg=m\frac{v^{2}}{L}$。
联立解得：$F_{2}=3F_{0}-2F_{1}$，故图线斜率$k=-2$。
(2)
由$F_{2}=3F_{0}-2F_{1}$，纵截距$3F_{0}=14.7\,\text{N}$，解得$F_{0}=4.9\,\text{N}$。
(3)
已知$F_{2}=7.35\,\text{N}$，代入$F_{2}=3F_{0}-2F_{1}$得：$7.35=3×4.9-2F_{1}$，解得$F_{1}=3.675\,\text{N}$。
由$F_{1}=F_{0}\cos\theta$，得$\cos\theta=\frac{F_{1}}{F_{0}}=\frac{3.675}{4.9}=\frac{3}{4}$。
答案：
(1)$-2$；
(2)$4.9$；
(3)$\frac{3}{4}$