2025年衡水名师新作高一物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年衡水名师新作高一物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6.(多选)(2025·广东省广州市模拟)如图所示,在飞镖比赛中,某运动员先后两次将飞镖(可视为质点)从同一位置正对竖直固定靶上的O点水平抛出,抛出点到O点的水平距离为4L,第一次抛出的飞镖击中O点正下方的P点,第二次抛出的飞镖击中O点正下方的Q点。已知飞镖击中P点和Q点时速度大小相等,OP = L,不计空气阻力,重力加速度大小为g,则下列说法正确的是 (

A.第一次抛出的飞镖落到P点时的速度大小为$\sqrt{10gL}$
B.第一次抛出的飞镖在空中运动的时间为2$\sqrt{\frac{2L}{g}}$
C.第二次抛出飞镖时飞镖的初速度大小为2$\sqrt{gL}$
D.P、Q点间的距离为3L
AD
)
A.第一次抛出的飞镖落到P点时的速度大小为$\sqrt{10gL}$
B.第一次抛出的飞镖在空中运动的时间为2$\sqrt{\frac{2L}{g}}$
C.第二次抛出飞镖时飞镖的初速度大小为2$\sqrt{gL}$
D.P、Q点间的距离为3L
答案:
AD [AB.第一次抛出过程,竖直方向有 $ L = \frac{1}{2} g t_1^2 $,可得第一次抛出的飞镖在空中运动的时间为 $ t_1 = \sqrt{\frac{2L}{g}} $,水平方向有 $ 4L = v_1 t_1 $,解得第一次抛出飞镖的初速度为 $ v_1 = 2 \sqrt{2gL} $,则第一次抛出的飞镖落到P点时的速度大小为 $ v_P = \sqrt{v_1^2 + v_y^2} = \sqrt{v_1^2 + (g t_1)^2} = \sqrt{10gL} $,故A正确,B错误;C.第二次抛出过程,有 $ 4L = v_2 t_2 $, $ v_Q = \sqrt{v_2^2 + (g t_2)^2} = v_P = \sqrt{10gL} $,联立解得第二次抛出飞镖时飞镖的初速度大小为 $ v_2 = \sqrt{2gL} $,故C错误;D.由 $ 4L = v_2 t_2 $, $ h = \frac{1}{2} g t_2^2 $,联立解得 $ h = 4L $,P、Q点间的距离为 $ y = 4L - L = 3L $,故D正确。]
7.(2025·安徽省芜湖市高一期中)在真空环境内探测微粒在重力作用下运动的简化装置如图所示。P是一个微粒源,能持续水平向右发射质量相同、初速度不同的微粒。高度为h = 0.8m的探测屏AB竖直放置,离P点的水平距离为L = 4.0m,上端A与P点的高度差也为h,(g取$10m/s^2)。$则能被屏探测到的微粒的最大初速度是 (

A.6m/s
B.8m/s
C.10m/s
D.12m/s
C
)
A.6m/s
B.8m/s
C.10m/s
D.12m/s
答案:
C [分析可知,打在A点的微粒最大时竖直距离 $ h = \frac{1}{2} g t^2 $,解得 $ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 × 0.8}{10}} s = 0.4 s $ 最大初速度 $ v_0 = \frac{L}{t} = \frac{4.0}{0.4} m/s = 10 m/s $,故ABD错误,C正确。]
8.(2025·江西省九江市高一期中)如图,在一个足够长的斜面上,有很多个台阶,每一个台阶高均为15cm,宽均为20cm,从上到下将台阶标记为第1、第2、第3、……号台阶。现在从第一号台阶末端沿水平方向抛出一个小球,抛出的初速度为5m/s,小球在空中运动的轨迹平面与过抛出点的台阶纵切面在同一个竖直平面内,不计空气阻力,小球第一次将落在第n号台阶上。则n等于 ( )

A.17
B.18
C.19
D.20

A.17
B.18
C.19
D.20
答案:
D [如图作一条连接各端点的直线,只要小球越过该直线,则小球落到台阶上。设小球落到斜线上的时间为t,根据平抛规律,有水平方向 $ x = v_0 t $,竖直方向 $ y = \frac{1}{2} g t^2 $,依题意有 $ \frac{x}{y} = \frac{20}{15} = \frac{4}{3} $,解得 $ t = 0.75 s $,相应的水平距离 $ x = v_0 t = 5 × 0.75 m = 3.75 m $,则台阶数 $ n = \frac{3.75}{0.2} = 18.75 $,因小球从第1号台阶末端抛出,知小球抛出后首先落到的台阶为第20级台阶。故D正确,ABC错误。]
D [如图作一条连接各端点的直线,只要小球越过该直线,则小球落到台阶上。设小球落到斜线上的时间为t,根据平抛规律,有水平方向 $ x = v_0 t $,竖直方向 $ y = \frac{1}{2} g t^2 $,依题意有 $ \frac{x}{y} = \frac{20}{15} = \frac{4}{3} $,解得 $ t = 0.75 s $,相应的水平距离 $ x = v_0 t = 5 × 0.75 m = 3.75 m $,则台阶数 $ n = \frac{3.75}{0.2} = 18.75 $,因小球从第1号台阶末端抛出,知小球抛出后首先落到的台阶为第20级台阶。故D正确,ABC错误。]

(2025·山东师大附中高一月考)如图所示的光滑斜面长为l,宽为b,倾角为θ,一物块(可看成质点)沿斜面左上方顶点P以初速度v₀水平射入,恰好从底端Q点离开斜面,已知重力加速度为g。则 (
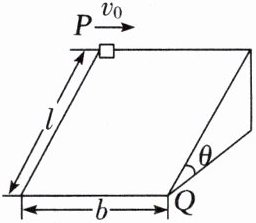
A.物块由P点变加速运动到Q点
B.物块由P点以加速度a = gcosθ匀加速运动到Q点
C.物块由P点运动到Q点所用的时间t = $\sqrt{\frac{2l}{g}}$
D.物块的初速度v₀ = b$\sqrt{\frac{g\sin\theta}{2l}}$
D
)
A.物块由P点变加速运动到Q点
B.物块由P点以加速度a = gcosθ匀加速运动到Q点
C.物块由P点运动到Q点所用的时间t = $\sqrt{\frac{2l}{g}}$
D.物块的初速度v₀ = b$\sqrt{\frac{g\sin\theta}{2l}}$
答案:
D [AB.依据物体做曲线运动的条件,初速度与合力方向垂直,且合力大小恒定,则物体做匀变速曲线运动,再根据牛顿第二定律得,物体的加速度为 $ a = \frac{mg \sin \theta}{m} = g \sin \theta $,故AB错误;C.根据 $ l = \frac{1}{2} a t^2 $,解得 $ t = \sqrt{\frac{2l}{a}} = \sqrt{\frac{2l}{g \sin \theta}} $,故C错误;D.根据 $ b = v_0 t $,解得 $ v_0 = \frac{b}{t} = \frac{b}{\sqrt{\frac{2l}{g \sin \theta}}} = b \sqrt{\frac{g \sin \theta}{2l}} $,故D正确。]
查看更多完整答案,请扫码查看


