《2025年学习质量监测八年级物理上册人教版》

2. (2024, 湖北) 我国古代把女子一拃长称为“咫”,男子一拃长称作“尺”,如图 1 - 1 - 5 所示。“咫尺之间”用来比喻相距很近,实际“咫”与“尺”的长度相差大约为(B)。

A.3 mm
B.3 cm
C.3 dm
D.3 m

答案： B 【解析】通常情况下,男子的手比女子的手大,一拃的长度也比女子的长一些。一拃长通常是20 cm左右,“咫”与“尺”的长度相差不会太大,3 mm过小,3 m过大,3 dm相当于30 cm也偏大,所以3 cm比较符合实际情况,即“咫”与“尺”的长度相差大约为3 cm。选项B正确。

3. (2022, 海南) 图 1 - 1 - 6 是戴在某普通学生手掌上的简易按摩仪,它的长度最接近(B)。

A.5 cm
B.15 cm
C.30 cm
D.40 cm

答案： B 【解析】从题图中可以看出,按摩仪的长度和手掌的长度大致相等,所以它的长度最接近15 cm。

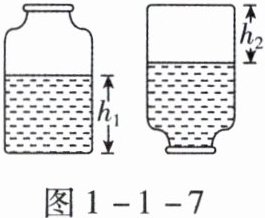
4. 如图 1 - 1 - 7 所示,一个饮料瓶装有多半瓶水,用刻度尺测出水的深度为 $ h_1 $,然后将该瓶倒置,水面到瓶底的高度为 $ h_2 $,若再用三角尺和刻度尺配合,测量瓶底的直径为 $ D $,那么,该瓶的容积大约为(A)。

A.$\frac{1}{4}\pi D^2 (h_1 + h_2)$
B.$\pi D^2 (h_1 + h_2)$
C.$4\pi D^2 (h_1 + h_2)$
D.$\pi D^2 (h_1 - h_2)$

答案： A 【解析】瓶正立时,水的体积$V_{1}=Sh_{1}$,S为瓶底面积。瓶倒置后,水面上方体积恰好为瓶正立时水面上方体积,这一体积用$V_{2}$表示,则$V_{2}=Sh_{2}$。由题图可知,瓶的容积为$V_{1}+V_{2}=Sh_{1}+Sh_{2}=S(h_{1}+h_{2})$。由于瓶底的直径为D,则瓶底的面积$S = π(\frac{D}{2})^{2}=\frac{1}{4}πD^{2}$,因此瓶的容积为$\frac{1}{4}πD^{2}(h_{1}+h_{2})$,选项A正确。

5. 现有一个圆柱形封闭油桶,形状如图 1 - 1 - 8 所示,在仅有一个钢卷尺(测量范围满足测量的要求)、一支粉笔和一个铅垂线,且不通过计算、不打开油桶的情况下,要求直接测量出封闭油桶的上、下边缘上两点间的最大直线距离,请设计一个实验方案,写出测量步骤。

答案：

(1)将油桶竖立在水平地面上,用粉笔沿桶底在水平地面上画一个圆;
(2)将油桶移至与所画圆相切的位置,设切点为$B'$,如图答1 - 1所示;
(3)利用铅垂线找出切点正上方油桶边缘上的点A;
(4)用钢卷尺找出过$B'$点的直径,确定直径的另一端点C的位置;
(5)用钢卷尺直接测量A、C之间的距离,即为油桶的上、下边缘上两点间的最大直线距离。