《2025年夺冠课课练九年级物理上册苏科版》

13. 如图甲所示,小华同学用水平力$F拉着木箱在水平方向上运动了距离L$,则小华对木箱所做的功$W_{1} = $$FL$.小莉同学用同样大小的力$F沿如图乙所示的斜面拉着同样的木箱在力的方向上也运动了距离L$,小莉对木箱所做的功为$W_{2}$,则$W_{2}$$=$(填"$＞$""$ = $"或"$＜$")$W_{1}$.

答案： $FL$ =

14. 生活中,人们通常用两种方法来比较做功的快慢.方法①:相同的时间比较做功的多少;方法②:做相同的功比较所用时间的多少.如图所示,用挖土机挖土比人力挖土快得多,所用的是判断方法①(填"①"或"②"),物理学用功率描述做功的快慢,公式为$P= \frac{W}{t}$,这种方法与上述方法①(填"①"或"②")是相同的.

答案： 做相同的功比较所用时间的多少 ① ①

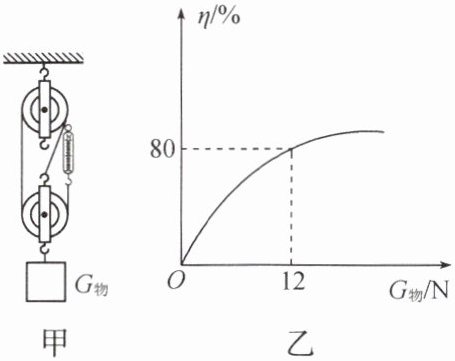
15. 现用如图甲所示的装置来探究滑轮组的机械效率$\eta与所挂物重G_{物}$的关系,改变$G_{物}$,竖直向上匀速拉动弹簧测力计,计算并绘出$\eta与G_{物}$关系如图乙所示,若不计绳重和摩擦,则:动滑轮自重为____3$N$;图乙中曲线表明,同一滑轮组的机械效率$\eta随所挂物重G_{物}$的增大而增大,最终____不会(填"会"或"不会")达到$100\%$;仅改变图甲中的绕绳方式、重复上述实验,所得到的$\eta - G_{物}$图线与图乙所示曲线____相同(填"相同"或"不同").

答案： 3 不会 相同

16. 小明用滑轮组提升物体,物体竖直移动的距离随时间变化的关系如图中图线甲所示,绳子自由端竖直移动的距离随时间变化的关系如图中图线乙所示.已知物体的质量为$90kg$,绳子自由端的拉力$F为260N$,$g取10N/kg$.不计绳重和摩擦,在$0\sim4s$的过程中,则:

(1) 滑轮组对物体做的有用功是多少?
(2) 拉力$F$做功的功率是多少?
(3) 用该滑轮组提升重为$660N$的物体时,滑轮组的机械效率是多少?

答案： 解:
(1)物体的重力$G=mg=90\ \text{kg}×10\ \text{N/kg}=900\ \text{N}$,滑轮组对物体做的有用功$W_{有用}=Gh=900\ \text{N}×0.1\ \text{m}=90\ \text{J}$.
(2)由图线乙可知,$t=4\ \text{s}$时,绳子自由端竖直移动的距离$s=40\ \text{cm}=0.4\ \text{m}$,拉力$F$做的功$W_{总}=Fs=260\ \text{N}×0.4\ \text{m}=104\ \text{J}$,拉力$F$的功率$P=\frac{W_{总}}{t}=\frac{104\ \text{J}}{4\ \text{s}}=26\ \text{W}$.
(3)由$s=nh$可得,滑轮组绳子的有效股数$n=\frac{s}{h}=\frac{40\ \text{cm}}{10\ \text{cm}}=4$,不计绳重和摩擦,由$F=\frac{1}{n}(G+G_{动})$可得,动滑轮的重力$G_{动}=nF-G=4×260\ \text{N}-900\ \text{N}=140\ \text{N}$,当提升重为660 N的物体时,滑轮组的机械效率$\eta=\frac{W'_{有用}}{W'_{总}}×100\%=\frac{G'h'}{(G'+G_{动})h'}×100\%=\frac{G'}{G'+G_{动}}×100\%=\frac{660\ \text{N}}{660\ \text{N}+140\ \text{N}}×100\% =82.5\%$.