《2025年夺冠课课练九年级物理上册苏科版》

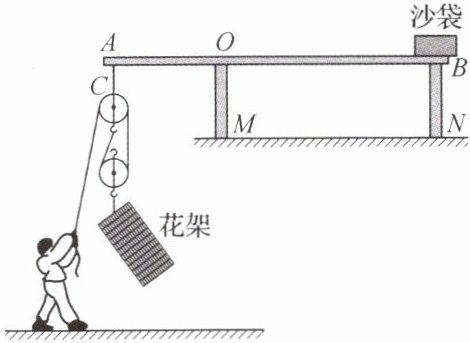
4. (2022·山东威海·统考中考真题)为了建设精致城市,每到春天园林工人要在过街天桥上放置花草,为城市增添一抹绿色.如图所示,工人用长木棒、滑轮、轻绳组装提升装置.木棒放置在天桥栏杆上始终保持水平,与栏杆$M接触点为O$；用沙袋将木棒$B端压在栏杆N$上,在木棒$A$端吊装滑轮组.$OA:OB = 1:2$,每个沙袋重$300\mathrm{\ N}$,每个滑轮重$24\mathrm{\ N}$(木棒和绳的重力、滑轮与轴的摩擦均忽略不计).
(1)若$A点受到竖直向下的拉力为1000\mathrm{\ N}$,为了保持木棒水平平衡,在$B$端至少需要放置几个沙袋？
(2)若某次工人利用滑轮组竖直向下拉绳子,将重为$376\mathrm{\ N}的花架匀速提升5\mathrm{\ m}$.求：
①滑轮组的机械效率；
②滑轮组对绳$AC$的拉力.

答案： 4. 解:
(1)木棒始终水平平衡且不计木棒的重力,由公式
$F_{A}l_{OA}=F_{B}l_{OB}$可知,木棒 B 端受到的压力为
$F_{B}=\frac {F_{A}l_{OA}}{l_{OB}}=\frac {1000N×1}{2}=500N$
沙袋的个数为
$n=\frac {500N}{300N}\approx 2$
所以在 B 端至少需要放置 2 个沙袋.
(2)①竖直匀速提升物体,绳的重力及滑轮与轴的摩擦均忽略不计,有用功为
$W_{有用}=G_{物}h=376N×5m=1880J$
额外功为
$W_{额外}=G_{动}h=24N×5m=120J$
总功为
$W_{总}=W_{有用}+W_{额外}=1880J+120J=2000J$
滑轮组的机械效率为
$η=\frac {W_{有用}}{W_{总}}×100\% =\frac {1880J}{2000J}×100\% =94\% .$
②因为竖直匀速提升,所以受力平衡,绳的重力及滑轮与轴的摩擦均忽略不计,动滑轮上绳子段数$n=2$,人的拉力为
$F_{拉}=\frac {G_{物}+G_{动}}{2}=\frac {376N+24N}{2}=200N$
滑轮组对绳 AC 的拉力
$F_{AC}=3F_{拉}+G_{定}=3×200N+24N=624N.$

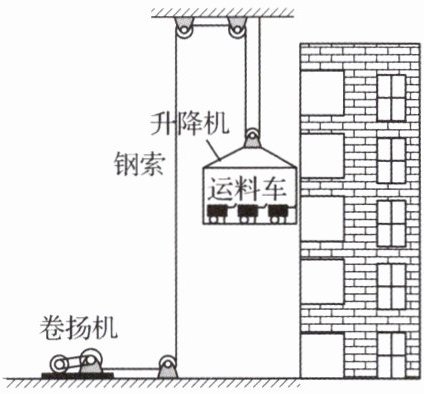
5. (2023·河南周口·统考三模)在房屋建筑的施工工地,工人常常使用一种电动卷扬机将建筑材料和工具提升送到各个楼层.如图所示是某建筑工地所使用的卷扬机的整个传动装置示意图,卷扬机通过滑轮将载有运料车的升降机提升到高处.若升降机匀速上升,将$3辆运料车由地面运送到6\mathrm{\ m}高的3$层楼上,钢索拉力大小为$F_{1}$,卷扬机的机械效率为$\eta_{1}$；卸出$2辆车接着将最后一辆车匀速运送到12\mathrm{\ m}高的5$层楼上,钢索拉力大小为$F_{2}$,卷扬机的机械效率为$\eta_{2}$.已知每辆运料车的质量$m = 100\mathrm{\ kg}$,$F_{1}:F_{2} = 5:3$,滑轮的摩擦和钢索的重力可忽略不计,$g取10\mathrm{\ N/kg}$.求：
(1)$\eta_{1}与\eta_{2}$的比值；
(2)在整个上升过程中钢索的拉力做的功；
(3)若每次升降机提升$3$辆运料车,卷扬机所使用的电动机的机械输出功率为$8\mathrm{\ kW}$,电动机输出的机械功率有$75\%$转化为钢索拉力做功的功率,则卷扬机带动升降机匀速上升的最大速度为多少.

答案： 5. 解:
(1)由图可知,承担物重的绳子段数$n=2$,由$η=\frac {W_{有用}}{W_{总}}×$
$100\% =\frac {Gh}{Fs}×100\% =\frac {Gh}{Fnh}×100\% =\frac {G}{Fn}×100\% $可知,两次
的机械效率分别为
$η_{1}=\frac {3mg}{2F_{1}}×100\% $
$η_{2}=\frac {mg}{2F_{2}}×100\% $
因为$F_{1}:F_{2}=5:3$,则
$\frac {η_{1}}{η_{2}}=\frac {\frac {3mg}{2F_{1}}×100\% }{\frac {mg}{2F_{2}}×100\% }=\frac {3F_{2}}{F_{1}}=3×\frac {3}{5}=\frac {9}{5}.$
(2)设升降机和动滑轮的总重为 G,所以
$F_{1}=\frac {1}{2}(3mg+G)$
$F_{2}=\frac {1}{2}(mg+G)$
因为$F_{1}:F_{2}=5:3$,则
$\frac {F_{1}}{F_{2}}=\frac {\frac {1}{2}(3mg+G)}{\frac {1}{2}(mg+G)}=\frac {5}{3}$
解得$G=2mg=2×100kg×10N/kg=2000N$.所以
$F_{1}=\frac {1}{2}(3mg+G)=\frac {1}{2}×(3×100kg×10N/kg+2000N)$
$=2500N$
$F_{2}=\frac {1}{2}(mg+G)=\frac {1}{2}×(100kg×10N/kg+2000N)$
$=1500N$
在整个上升过程中钢索的拉力做的功为
$W=W_{1}+W_{2}=2F_{1}h+2F_{2}h=2×2500N×6m+2×$
$1500N×6m=4.8×10^{4}J.$
(3)电动机对钢索拉力做功的功率为
$P=75\% ×P_{出}=75\% ×8000W=6000W$
由$P=Fv$可知,卷扬机带动升降机上升的最大速度为
$v=\frac {P}{F}=\frac {P}{G_{总}}=\frac {6000W}{3×100kg×10N/kg+2000N}=1.2m/s.$