《2025年暑假生活河北美术出版社五年级数学》

2. 按要求画图。
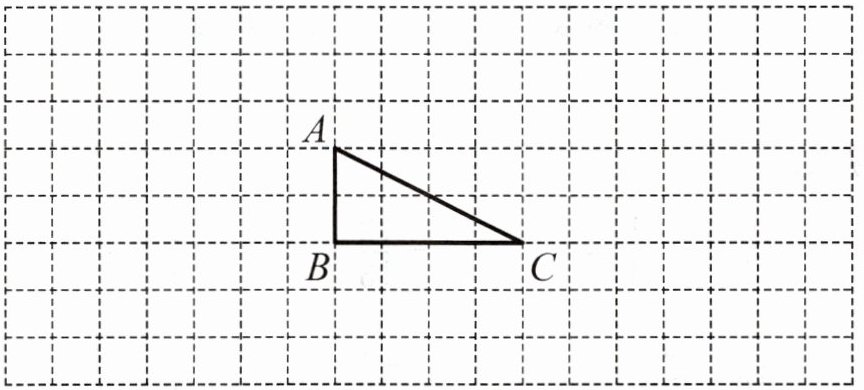
(1)把三角形 ABC 绕点 B 逆时针旋转$90^{\circ }$,得到图①。连接$AB$、$BC$。以点$B$为旋转中心，将$BA$绕点$B$逆时针旋转$90^{\circ}$，根据网格特点确定$A$点旋转后的对应点$A_1$的位置（因为是在网格中，$BA$是垂直方向的线段，绕$B$逆时针旋转$90^{\circ}$后变为水平向左的线段，长度不变）。$BC$绕点$B$逆时针旋转$90^{\circ}$，确定$C$点旋转后的对应点$C_1$的位置（$BC$是水平方向的线段，绕$B$逆时针旋转$90^{\circ}$后变为垂直向上的线段，长度不变）。连接$A_1B$、$B C_1$、$A_1C_1$，得到三角形$A_1BC_1$，即图①。
(2)把三角形 ABC 绕点 C 顺时针旋转$90^{\circ }$,得到图②。以点$C$为旋转中心，将$CA$绕点$C$顺时针旋转$90^{\circ}$，根据网格特点确定$A$点旋转后的对应点$A_2$的位置（$CA$是斜线段，绕$C$顺时针旋转$90^{\circ}$，可通过构建直角三角形，利用网格边长确定其位置）。$CB$绕点$C$顺时针旋转$90^{\circ}$，确定$B$点旋转后的对应点$B_2$的位置（$CB$是水平方向的线段，绕$C$顺时针旋转$90^{\circ}$后变为垂直向下的线段，长度不变）。连接$A_2C$、$C B_2$、$A_2B_2$，得到三角形$A_2CB_2$，即图②。

答案： 本题可根据旋转的性质来画图。
步骤一：明确旋转的性质
在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转。这个定点叫做旋转中心，转动的角度叫做旋转角。旋转的性质有：
对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
旋转前、后的图形全等。
步骤二：画出绕点$B$逆时针旋转$90^{\circ}$后的图形①
连接$AB$、$BC$。
以点$B$为旋转中心，将$BA$绕点$B$逆时针旋转$90^{\circ}$，根据网格特点确定$A$点旋转后的对应点$A_1$的位置（因为是在网格中，$BA$是垂直方向的线段，绕$B$逆时针旋转$90^{\circ}$后变为水平向左的线段，长度不变）。
$BC$绕点$B$逆时针旋转$90^{\circ}$，确定$C$点旋转后的对应点$C_1$的位置（$BC$是水平方向的线段，绕$B$逆时针旋转$90^{\circ}$后变为垂直向上的线段，长度不变）。
连接$A_1B$、$B C_1$、$A_1C_1$，得到三角形$A_1BC_1$，即图①。
步骤三：画出绕点$C$顺时针旋转$90^{\circ}$后的图形②
以点$C$为旋转中心，将$CA$绕点$C$顺时针旋转$90^{\circ}$，根据网格特点确定$A$点旋转后的对应点$A_2$的位置（$CA$是斜线段，绕$C$顺时针旋转$90^{\circ}$，可通过构建直角三角形，利用网格边长确定其位置）。
$CB$绕点$C$顺时针旋转$90^{\circ}$，确定$B$点旋转后的对应点$B_2$的位置（$CB$是水平方向的线段，绕$C$顺时针旋转$90^{\circ}$后变为垂直向下的线段，长度不变）。
连接$A_2C$、$C B_2$、$A_2B_2$，得到三角形$A_2CB_2$，即图②。
综上，按照上述方法即可画出满足要求的图①和图②。（由于是画图题，此处无法直接呈现图形，你可根据上述步骤在给定的网格图中进行绘制）

1. 王老师一天中大约有$\frac{3}{8}$的时间用于睡眠,$\frac{1}{8}$的时间用于进餐,$\frac{1}{6}$的时间用于活动,其他的时间用于工作和学习。
(1)照这样计算,他每天用于睡眠、进餐和活动的时间一共占一天时间的几分之几?
(2)王老师用于工作和学习的时间比活动的时间多占一天时间的几分之几?

答案：
(1) $\frac{3}{8}+\frac{1}{8}+\frac{1}{6}=\frac{2}{3}$
(2) $1-\frac{2}{3}=\frac{1}{3}$ $\frac{1}{3}-\frac{1}{6}=\frac{1}{6}$

2. 有一张长方形的纸,长 72 cm,宽 48 cm。小丽要用它剪成若干同样大小的正方形纸,而且没有剩余。如果想要剪出最大的正方形,那么剪出的每张正方形纸的边长应是多少厘米? 可以剪成几个这样的正方形?

答案： $72=2×2×2×3×3$ $48=2×2×2×2×3$ 72 和 48 的最大公因数是 $2×2×2×3=24$ 边长为 24 cm 正方形个数: $(72÷24)×(48÷24)=6$ (个)

3. 一个正方体玻璃容器,从里面量长、宽均为 20 cm,向容器中倒入 6 L 水,再把一个土豆放入水中,这时量得容器内的水深是 17 cm。这个土豆的体积是多少立方分米?

答案： $6L=6000cm³$ $20×20×17-6000=800(cm³)$ $800cm³=0.8dm³$