2025年暑假大串联八年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假大串联八年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
13. 如图,直线$a // b$,点$B$在直线$b$上,且$AB \perp BC$,$\angle 1 = 55^{\circ}$,则$\angle 2$的度数为(
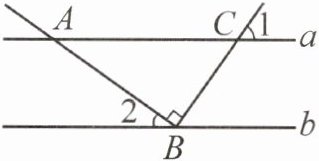
A. $35^{\circ}$
B. $45^{\circ}$
C. $55^{\circ}$
D. $125^{\circ}$
A
) 
A. $35^{\circ}$
B. $45^{\circ}$
C. $55^{\circ}$
D. $125^{\circ}$
答案:
A
14. 如果$m$是任意实数,则点$P(m - 4,m + 1)$一定不在(
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
D
)A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
答案:
D
15. 解不等式组.
$\begin{cases}2x + 5 \leq 3(x + 2)\\2x - \frac{1 + 3x}{2} < 1\end{cases}$
把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
$\begin{cases}2x + 5 \leq 3(x + 2)\\2x - \frac{1 + 3x}{2} < 1\end{cases}$
把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.
答案:
解:$\begin{cases}2x + 5 \leq 3(x + 2) & ① \\ 2x - \frac{1 + 3x}{2} < 1 & ②\end{cases}$ 解不等式①得:$x \geq -1$,解不等式②得:$x < 3$。所以原不等式组的解集是:$-1 \leq x < 3$。其解集在数轴上表示如下:$-2 -1 0 1 2 3 4 5$ 所以原不等式组的非负整数解有:0,1,2。
16. 为迎接上海世博会,举办知识竞赛,设一、二、三等奖共$12$名,奖品发放方案如下:
|一等奖|二等奖|三等奖|
|----|----|----|
|一盒“海宝”和一枚徽章|一盒“海宝”|一枚徽章|
用于购买奖品的总费用不少于$1000$元但不超过$1100$元,小明在购买“海宝”和徽章时了解到如下信息:两盒“海宝”与一枚徽章共$315$元,一盒“海宝”与三枚徽章共$195$元.
(1)求一盒“海宝”和一枚徽章各多少元;
(2)本次活动一等奖$2$名,则二等奖和三等奖应各有多少名?
|一等奖|二等奖|三等奖|
|----|----|----|
|一盒“海宝”和一枚徽章|一盒“海宝”|一枚徽章|
用于购买奖品的总费用不少于$1000$元但不超过$1100$元,小明在购买“海宝”和徽章时了解到如下信息:两盒“海宝”与一枚徽章共$315$元,一盒“海宝”与三枚徽章共$195$元.
(1)求一盒“海宝”和一枚徽章各多少元;
(2)本次活动一等奖$2$名,则二等奖和三等奖应各有多少名?
答案:
解:
(1)设一盒“海宝”为$x$元,一枚徽章为$y$元,$\begin{cases}2x + y = 315 \\ x + 3y = 195\end{cases}$,解得$\begin{cases}x = 150 \\ y = 15\end{cases}$。
(2)设二等奖为$m$名,则三等奖为$(12 - 2 - m)$名,$\begin{cases}2 \times 165 + 150m + 15(10 - m) \geq 1000 \\ 2 \times 165 + 150m + 15(10 - m) \leq 1100\end{cases}$,解得:$3.85 \leq m \leq 4.59$。又$m$为整数,所以$m = 4$,则$10 - m = 6$。答:二等奖为4名,三等奖为6名。
(1)设一盒“海宝”为$x$元,一枚徽章为$y$元,$\begin{cases}2x + y = 315 \\ x + 3y = 195\end{cases}$,解得$\begin{cases}x = 150 \\ y = 15\end{cases}$。
(2)设二等奖为$m$名,则三等奖为$(12 - 2 - m)$名,$\begin{cases}2 \times 165 + 150m + 15(10 - m) \geq 1000 \\ 2 \times 165 + 150m + 15(10 - m) \leq 1100\end{cases}$,解得:$3.85 \leq m \leq 4.59$。又$m$为整数,所以$m = 4$,则$10 - m = 6$。答:二等奖为4名,三等奖为6名。
17. 在如图的直角坐标系中,将$\triangle ABC$平移后得到$\triangle A'B'C'$,它们的各顶点坐标如下表所示:
|$\triangle ABC$|$A(a,0)$|$B(3,0)$|$C(5,5)$|
|----|----|----|----|
|$\triangle A'B'C'$|$A'(4,2)$|$B'(7,b)$|$C'(c,d)$|
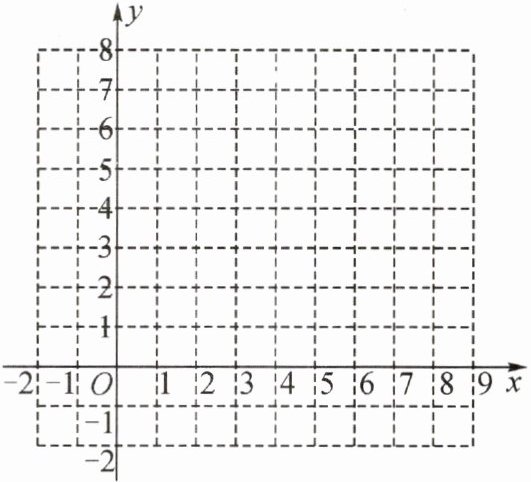
(1)观察表中各对应点坐标的变化,并填空:$\triangle ABC$向____平移____个单位长度,再向____平移____个单位长度可以得到$\triangle A'B'C'$;
(2)在坐标系中画出$\triangle ABC$及平移后的$\triangle A'B'C'$;
(3)求出$\triangle A'B'C'$的面积.
|$\triangle ABC$|$A(a,0)$|$B(3,0)$|$C(5,5)$|
|----|----|----|----|
|$\triangle A'B'C'$|$A'(4,2)$|$B'(7,b)$|$C'(c,d)$|

(1)观察表中各对应点坐标的变化,并填空:$\triangle ABC$向____平移____个单位长度,再向____平移____个单位长度可以得到$\triangle A'B'C'$;
(2)在坐标系中画出$\triangle ABC$及平移后的$\triangle A'B'C'$;
(3)求出$\triangle A'B'C'$的面积.
答案:
解:
(1)上 2 右 4
(2)如图:

(3)$S_{\triangle A'B'C'} = S_{\triangle ABC} = \frac{1}{2}AB \times y_C = \frac{1}{2} \times 3 \times 5 = 7.5$。
解:
(1)上 2 右 4
(2)如图:

(3)$S_{\triangle A'B'C'} = S_{\triangle ABC} = \frac{1}{2}AB \times y_C = \frac{1}{2} \times 3 \times 5 = 7.5$。
查看更多完整答案,请扫码查看


