2025年暑假作业南方出版社四年级数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假作业南方出版社四年级数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
2. 画一个底边是4厘米,高是2厘米的等腰三角形。
答案:
【解析】:
1. 首先画一条线段$AB = 4$厘米,作为等腰三角形的底边。
2. 然后作线段$AB$的垂直平分线:
分别以$A$、$B$为圆心,大于$\frac{1}{2}AB$(即大于$2$厘米)的长度为半径画弧,两弧分别相交于上下两点。
连接这两个交点,得到线段$AB$的垂直平分线。
3. 在垂直平分线上截取$OC = 2$厘米($O$为$AB$中点),点$C$就是等腰三角形的顶点。
4. 最后连接$AC$和$BC$,$\triangle ABC$就是所求的底边是$4$厘米,高是$2$厘米的等腰三角形。
【答案】:先画一条$4$厘米的线段作为底边,作其垂直平分线,在垂直平分线上截取$2$厘米确定顶点,连接顶点与底边两端点得到等腰三角形(需按此步骤实际画图)。
【解析】:
1. 首先画一条线段$AB = 4$厘米,作为等腰三角形的底边。
2. 然后作线段$AB$的垂直平分线:
分别以$A$、$B$为圆心,大于$\frac{1}{2}AB$(即大于$2$厘米)的长度为半径画弧,两弧分别相交于上下两点。
连接这两个交点,得到线段$AB$的垂直平分线。
3. 在垂直平分线上截取$OC = 2$厘米($O$为$AB$中点),点$C$就是等腰三角形的顶点。
4. 最后连接$AC$和$BC$,$\triangle ABC$就是所求的底边是$4$厘米,高是$2$厘米的等腰三角形。
【答案】:先画一条$4$厘米的线段作为底边,作其垂直平分线,在垂直平分线上截取$2$厘米确定顶点,连接顶点与底边两端点得到等腰三角形(需按此步骤实际画图)。

五、求三角形中未知角的度数。


答案:
180°-25°-113°=42°
180°-75°-45°=60°
180°-20°-133°=27°
90°-56°=34°
180°-75°-45°=60°
180°-20°-133°=27°
90°-56°=34°
1. 三角形ABC的周长是78厘米,$\angle B=\angle C$,$BC = 14$厘米,求AB的长。


答案:
【解析】:因为$\angle B = \angle C$,所以三角形$ABC$是等腰三角形,$AB = AC$。
已知三角形$ABC$周长是$78$厘米,$BC = 14$厘米,根据等腰三角形周长公式$周长=AB + AC+BC$,又因为$AB = AC$,所以$AB=(周长 - BC)\div2=(78 - 14)\div2 = 32$(厘米)。
【答案】:$32$厘米
已知三角形$ABC$周长是$78$厘米,$BC = 14$厘米,根据等腰三角形周长公式$周长=AB + AC+BC$,又因为$AB = AC$,所以$AB=(周长 - BC)\div2=(78 - 14)\div2 = 32$(厘米)。
【答案】:$32$厘米
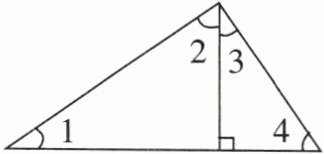
2. 右下图的三角形中,$\angle 1 = 35^{\circ}$,$\angle 2+\angle 3 = 90^{\circ}$,求$\angle 2$、$\angle 3$和$\angle 4$的度数。

答案:
【解析】:
在左边小直角三角形中,因为三角形内角和为$180^{\circ}$,其中一个角是$90^{\circ}$,$\angle1 = 35^{\circ}$,所以$\angle2=180^{\circ}-90^{\circ}-\angle1$,即$\angle2 = 180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
又因为$\angle2+\angle3 = 90^{\circ}$,所以$\angle3=90^{\circ}-\angle2$,$\angle3 = 90^{\circ}-55^{\circ}=35^{\circ}$。
在右边小直角三角形中,根据三角形内角和为$180^{\circ}$,一个角是$90^{\circ}$,$\angle3 = 35^{\circ}$,所以$\angle4=180^{\circ}-90^{\circ}-\angle3$,即$\angle4 = 180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
【答案】:$\angle2 = 55^{\circ}$,$\angle3 = 35^{\circ}$,$\angle4 = 55^{\circ}$。
在左边小直角三角形中,因为三角形内角和为$180^{\circ}$,其中一个角是$90^{\circ}$,$\angle1 = 35^{\circ}$,所以$\angle2=180^{\circ}-90^{\circ}-\angle1$,即$\angle2 = 180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
又因为$\angle2+\angle3 = 90^{\circ}$,所以$\angle3=90^{\circ}-\angle2$,$\angle3 = 90^{\circ}-55^{\circ}=35^{\circ}$。
在右边小直角三角形中,根据三角形内角和为$180^{\circ}$,一个角是$90^{\circ}$,$\angle3 = 35^{\circ}$,所以$\angle4=180^{\circ}-90^{\circ}-\angle3$,即$\angle4 = 180^{\circ}-90^{\circ}-35^{\circ}=55^{\circ}$。
【答案】:$\angle2 = 55^{\circ}$,$\angle3 = 35^{\circ}$,$\angle4 = 55^{\circ}$。
七、数学小博士。
如右图,求$\angle 1$是多少度。
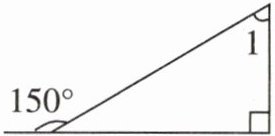
如右图,求$\angle 1$是多少度。

答案:
【解析】:
1. 首先求与$150^{\circ}$角相邻的内角:
因为平角是$180^{\circ}$,所以与$150^{\circ}$角相邻的内角为$180 - 150=30^{\circ}$。
2. 然后根据直角三角形内角和是$180^{\circ}$(其中一个角是$90^{\circ}$)求$\angle1$:
已知三角形内角和为$180^{\circ}$,在这个直角三角形中,$\angle1=180 - 90 - 30$。
先算$180 - 90 = 90$,再算$90 - 30 = 60^{\circ}$。
【答案】:$60^{\circ}$
1. 首先求与$150^{\circ}$角相邻的内角:
因为平角是$180^{\circ}$,所以与$150^{\circ}$角相邻的内角为$180 - 150=30^{\circ}$。
2. 然后根据直角三角形内角和是$180^{\circ}$(其中一个角是$90^{\circ}$)求$\angle1$:
已知三角形内角和为$180^{\circ}$,在这个直角三角形中,$\angle1=180 - 90 - 30$。
先算$180 - 90 = 90$,再算$90 - 30 = 60^{\circ}$。
【答案】:$60^{\circ}$
查看更多完整答案,请扫码查看


