《2025年一本暑假衔接五升六数学人教版浙江专版》

3. 计算下面各立体图形的表面积和体积。(单位:cm)

答案： 3.
(1)表面积:$(17×6+17×9+6×9)×2=618(cm^{2})$
体积:$17×9×6=918(cm^{3})$
(2)表面积:$20×8×4+8×8×2+4×4×4=832(cm^{2})$
体积:$20×8×8+4×4×4=1344(cm^{3})$

4. 用一根长84cm的铁丝做一个长方体框架,做成的长方体框架长、宽、高的厘米数是3个连续的自然数。这个长方体的体积是多少立方厘米?

答案： 4. $84÷4÷3=7(cm)$
$7+1=8(cm)$
$7-1=6(cm)$
$7×8×6=336(cm^{3})$
答:这个长方体的体积是$336cm^{3}$。

5. (北京·海淀)笑笑家有甲、乙两个不同规格的带盖收纳盒,她想把家里散落的小包纸巾分别放入这两个收纳盒中(纸巾不能超过收纳盒的上沿且不能挤压)。一小包纸巾的长、宽、高和甲、乙两个收纳盒的长、宽、高如下图所示(收纳盒制作材料的厚度忽略不计)。(单位:cm)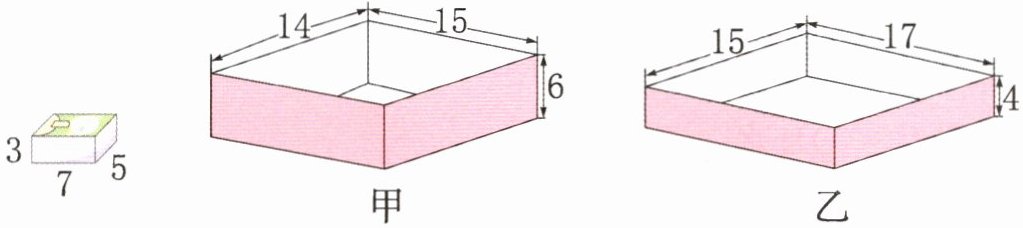 
(1)甲收纳盒中最多可以放置多少包纸巾?
(2)尽可能多地往乙收纳盒中放纸巾,可以放置多少包?
结合生活实际,我()(填“同意”或“不同意”)笑笑的想法。如果同意,请你写出理由;如果不同意,尽可能多地往乙收纳盒中放纸巾,可以放置多少包?写出你的思考过程。

答案： 5.
(1)$(15÷5)×(14÷7)×(6÷3)=12$(包)
答:甲收纳盒中最多可以放置 12 包纸巾。
(2)不同意
$15÷5=3$(包)
$17-7=10(cm)$
$10÷5=2$(包)
$15÷7=2$(包)$\cdots \cdots 1(cm)$
$2×2+3=7$(包)
答:可以放置7包。