第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
4 一个等腰三角形的顶角是一个底角的4倍,这个等腰三角形的底角和顶角分别是多少度?
答案:
解:设这个等腰三角形的底角为$x$度,则顶角为$4x$度。
因为等腰三角形两底角相等,三角形内角和为$180^{\circ}$,所以可得方程:
$x + x + 4x = 180$
$6x = 180$
$x = 30$
顶角为:$4x = 4×30 = 120$(度)
底角:$30^{\circ}$,顶角:$120^{\circ}$
因为等腰三角形两底角相等,三角形内角和为$180^{\circ}$,所以可得方程:
$x + x + 4x = 180$
$6x = 180$
$x = 30$
顶角为:$4x = 4×30 = 120$(度)
底角:$30^{\circ}$,顶角:$120^{\circ}$
巧数三角形
数三角形比数长方形、正方形显得复杂,随着构图形式的变化,难度也更大。如:
(1)下图中共有多少个三角形?
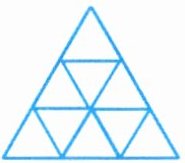
解:我们把图中最短的线段称为“一个单位长度”,这样按顺序数下去:
①以一个单位长度为边的三角形有:正6个,倒3个,共9个。
②以两个单位长度为边的三角形有3个。
③以三个单位长度为边的三角形有1个。
$9+3+1= 13$(个),全图总共有13个三角形。
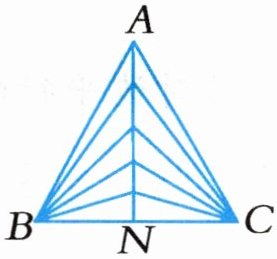
(2)数数下图共有多少个三角形。
数三角形比数长方形、正方形显得复杂,随着构图形式的变化,难度也更大。如:
(1)下图中共有多少个三角形?

解:我们把图中最短的线段称为“一个单位长度”,这样按顺序数下去:
①以一个单位长度为边的三角形有:正6个,倒3个,共9个。
②以两个单位长度为边的三角形有3个。
③以三个单位长度为边的三角形有1个。
$9+3+1= 13$(个),全图总共有13个三角形。
(2)数数下图共有多少个三角形。

答案:
解:按三角形顶点方向分类计数:
①顶点向上的三角形:
以1个单位长度为边:5+4+3+2+1=15(个)
②顶点向下的三角形:
以1个单位长度为边:4+3+2+1=10(个)
以2个单位长度为边:3+2+1=6(个)
以3个单位长度为边:2+1=3(个)
以4个单位长度为边:1(个)
③中间五边形内的三角形:5(个)
总个数:15+10+6+3+1+5=35(个)
答:共有35个三角形。
①顶点向上的三角形:
以1个单位长度为边:5+4+3+2+1=15(个)
②顶点向下的三角形:
以1个单位长度为边:4+3+2+1=10(个)
以2个单位长度为边:3+2+1=6(个)
以3个单位长度为边:2+1=3(个)
以4个单位长度为边:1(个)
③中间五边形内的三角形:5(个)
总个数:15+10+6+3+1+5=35(个)
答:共有35个三角形。
查看更多完整答案,请扫码查看


