一、直接写得数。
$30×90=
$1.2-0.9=
$30×90=
2700
$ $70×40=2800
$ $4200÷7=600
$ $280÷7=40
$$1.2-0.9=
0.3
$ $5.7+0.8=6.5
$ $30×200=6000
$ $450+85=535
$
答案:
分析:
这些题目都是基础的数学运算题目,包括乘法、除法、加法和减法。
对于乘法题目,可以直接使用乘法口诀或者乘法运算规则进行计算。
对于除法题目,需要确定商的位置以及余数的处理。
对于加法题目,注意相同数位对齐,从个位加起,哪一位上的数相加满十,就向前一位进一。
对于减法题目,注意相同数位对齐,从个位减起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减。
答案:
$30×90 = 2700$
$70×40 = 2800$
$4200÷7 = 600$
$280÷7 = 40$
$1.2 - 0.9 = 0.3$
$5.7 + 0.8 = 6.5$
$30×200 = 6000$
$450 + 85 = 535$
这些题目都是基础的数学运算题目,包括乘法、除法、加法和减法。
对于乘法题目,可以直接使用乘法口诀或者乘法运算规则进行计算。
对于除法题目,需要确定商的位置以及余数的处理。
对于加法题目,注意相同数位对齐,从个位加起,哪一位上的数相加满十,就向前一位进一。
对于减法题目,注意相同数位对齐,从个位减起,哪一位上的数不够减,就从它的前一位退一作十,和本位上的数合并在一起,再减。
答案:
$30×90 = 2700$
$70×40 = 2800$
$4200÷7 = 600$
$280÷7 = 40$
$1.2 - 0.9 = 0.3$
$5.7 + 0.8 = 6.5$
$30×200 = 6000$
$450 + 85 = 535$
二、判断正误。(对的画“√”,错的画“×”)
1. 一个边长是 4 厘米的正方形,它的周长和面积相等。(
2. 如果两个正方形的面积相等,那么它们的边长和周长一定都相等。(
3. 一个长方形,长 5 分米、宽 4 分米,它的面积是 20 分米。(
4. 小平家距离学校 680 平方米远。(
1. 一个边长是 4 厘米的正方形,它的周长和面积相等。(
×
)2. 如果两个正方形的面积相等,那么它们的边长和周长一定都相等。(
√
)3. 一个长方形,长 5 分米、宽 4 分米,它的面积是 20 分米。(
×
)4. 小平家距离学校 680 平方米远。(
×
)
答案:
解析:
1. 题目考查了正方形周长和面积的计算及单位理解。周长是正方形四边之和,面积是边长的平方。虽然计算结果都是16,但单位不同,意义不同,不能直接比较。
答案:
×
2. 题目考查了正方形面积与边长的关系。如果两个正方形的面积相等,那么它们的边长一定相等,进而周长也相等。
答案:
√
3. 题目考查了长方形面积的计算。长方形的面积是长乘以宽,但面积的单位应该是平方分米,而不是分米。
答案:
×
4. 题目考查了距离的单位理解。描述距离时,应使用长度单位,如米、千米等,而不是面积单位平方米。
答案:
×
1. 题目考查了正方形周长和面积的计算及单位理解。周长是正方形四边之和,面积是边长的平方。虽然计算结果都是16,但单位不同,意义不同,不能直接比较。
答案:
×
2. 题目考查了正方形面积与边长的关系。如果两个正方形的面积相等,那么它们的边长一定相等,进而周长也相等。
答案:
√
3. 题目考查了长方形面积的计算。长方形的面积是长乘以宽,但面积的单位应该是平方分米,而不是分米。
答案:
×
4. 题目考查了距离的单位理解。描述距离时,应使用长度单位,如米、千米等,而不是面积单位平方米。
答案:
×
三、在$◯$里填上“>”“<”或“=”。
$34×11$
$18×23$
$34×11$
<
$43×11$ $70×60$>
$50×80$ $12×34$<
$14×32$$18×23$
<
$32×18$ $27×40$=
$270×4$ $75×13$>
$82×11$
答案:
解析:本题考查了两位数乘两位数的计算及大小比较。
先计算出每个式子的结果,再比较大小。
$34×11 = 374$,$43×11 = 473$,$374<473$,所以$34×11<43×11$;
$70×60 = 4200$,$50×80 = 4000$,$4200>4000$,所以$70×60>50×80$;
$12×34 = 408$,$14×32 = 448$,$408<448$,所以$12×34<14×32$;
$18×23 = 414$,$32×18 = 576$,$414<576$,所以$18×23<32×18$;
$27×40 = 1080$,$270×4 = 1080$,$1080 = 1080$,所以$27×40 = 270×4$;
$75×13 = 975$,$82×11 = 902$,$975>902$,所以$75×13>82×11$。
答案:<;>;<;<;=;>。
先计算出每个式子的结果,再比较大小。
$34×11 = 374$,$43×11 = 473$,$374<473$,所以$34×11<43×11$;
$70×60 = 4200$,$50×80 = 4000$,$4200>4000$,所以$70×60>50×80$;
$12×34 = 408$,$14×32 = 448$,$408<448$,所以$12×34<14×32$;
$18×23 = 414$,$32×18 = 576$,$414<576$,所以$18×23<32×18$;
$27×40 = 1080$,$270×4 = 1080$,$1080 = 1080$,所以$27×40 = 270×4$;
$75×13 = 975$,$82×11 = 902$,$975>902$,所以$75×13>82×11$。
答案:<;>;<;<;=;>。
四、下面的计算对吗?对的画“√”,错的画“×”,并改正。
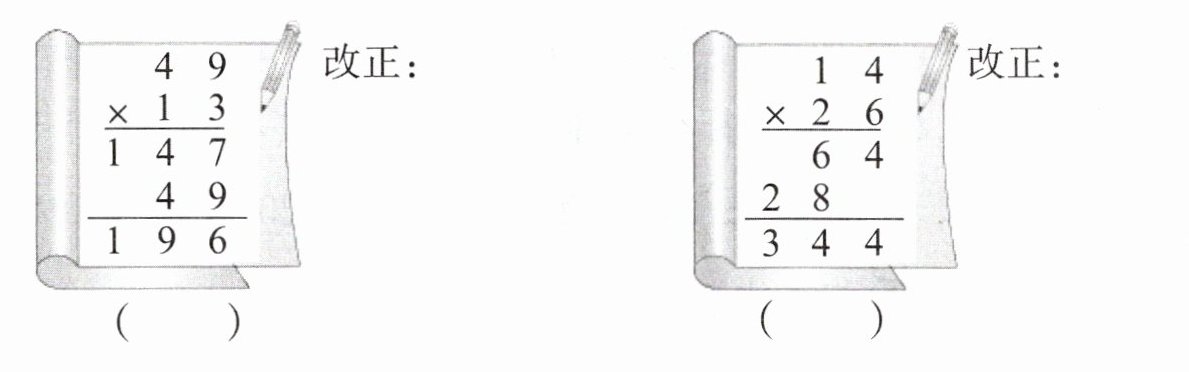

×
$\begin{aligned}&\quad\ \ 14\\&×\ 26\\&\overline{\quad\ 84}\\&\ 280\\&\overline{364}\end{aligned}$
答案:
本题可根据两位数乘两位数的计算方法来判断对错并改正。
1. 分析原计算过程
两位数乘两位数的计算方法:先用第二个乘数的个位去乘第一个乘数,得数的末位与乘数的个位对齐;再用第二个乘数的十位去乘第一个乘数,得数的末位与乘数的十位对齐;最后把两次乘得的积相加。
在计算$14×26$时,先计算$14×6 = 84$,再计算$14×20 = 280$,最后将两个结果相加,$84 + 280 = 364$。
而原计算过程中,在计算$14×20$时出现错误,$14×20$的结果应该是$280$,不是$28$,导致最终结果错误。
2. 判断对错并改正
原计算错误,应画“×”。
正确的计算过程如下:
$\begin{aligned}&\quad\ \ 14\\&×\ 26\\&\overline{\quad\ 84}\\&\ 280\\&\overline{364}\end{aligned}$
故答案为:×;
$\begin{aligned}&\quad\ \ 14\\&×\ 26\\&\overline{\quad\ 84}\\&\ 280\\&\overline{364}\end{aligned}$
1. 分析原计算过程
两位数乘两位数的计算方法:先用第二个乘数的个位去乘第一个乘数,得数的末位与乘数的个位对齐;再用第二个乘数的十位去乘第一个乘数,得数的末位与乘数的十位对齐;最后把两次乘得的积相加。
在计算$14×26$时,先计算$14×6 = 84$,再计算$14×20 = 280$,最后将两个结果相加,$84 + 280 = 364$。
而原计算过程中,在计算$14×20$时出现错误,$14×20$的结果应该是$280$,不是$28$,导致最终结果错误。
2. 判断对错并改正
原计算错误,应画“×”。
正确的计算过程如下:
$\begin{aligned}&\quad\ \ 14\\&×\ 26\\&\overline{\quad\ 84}\\&\ 280\\&\overline{364}\end{aligned}$
故答案为:×;
$\begin{aligned}&\quad\ \ 14\\&×\ 26\\&\overline{\quad\ 84}\\&\ 280\\&\overline{364}\end{aligned}$
查看更多完整答案,请扫码查看


