《2025年优秀生快乐假期每一天全新暑假作业本五年级数学人教版》

五、小明的依据是什么？
因为分成2组、3组或5组都没有同学被遗漏，所以总人数是2、3、5的公倍数。2、3、5两两互质，最小公倍数为2×3×5 = 30。又因为人数不足60，符合条件的公倍数只有30，所以这批同学有30人。

答案： 解：因为分成$2$组、$3$组或$5$组都没有同学被遗漏，所以总人数是$2$、$3$、$5$的公倍数。
$2$、$3$、$5$两两互质，根据最小公倍数公式$a$、$b$、$c$两两互质时，$LCM(a,b,c)=a× b× c$（$LCM$表示最小公倍数），可得$2$、$3$、$5$的最小公倍数为$2×3×5 = 30$。
又因为人数不足$60$，$2$、$3$、$5$的公倍数还有$30×2 = 60$（舍去），所以符合条件的公倍数只有$30$。
所以小明的依据是：总人数是$2$、$3$、$5$的公倍数且小于$60$，$2$、$3$、$5$的最小公倍数是$30$，所以这批同学有$30$人。

六、将两块正方形的地砖通过切割,拼成一个大正方形。
例：

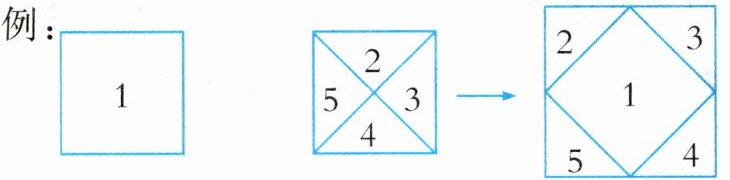
请画出另外一种切割方案：

答案：

翻转杯子
乐乐家里来了客人,妈妈从厨房端了7个杯子给大家倒茶。为了防止落灰,这些杯子都是杯口朝下摆放的。一位叔叔对乐乐说：“乐乐啊,叔叔来考考你。如果只允许你一次翻转4个杯子,经过多少次翻转后,这7个杯子的杯口才能都朝上呢？”
乐乐开始动手翻杯子,翻了半天也没能把杯口都翻过来。那位叔叔笑着问：“怎么样,有结果了吗？”乐乐略带委屈地说：“叔叔,根本不能同时翻转过来。”
“哈哈。”那位叔叔笑了,“这样吧,你再拿3个杯子来,还是一次只能翻4个杯子,看看这回翻几次之后杯口全部朝上。”乐乐又拿了3个杯子。这回,乐乐只翻了3次,10个杯子的杯口就全部朝上了。
乐乐有点弄不明白：“为什么7个杯子不行,10个杯子就可以呢？”
叔叔说：“那就要你自己思考啦。”

答案： 【解析】：对于一个杯子，杯口朝下变为杯口朝上需要翻转奇数次。设杯口朝下为状态$0$，杯口朝上为状态$1$。
- 当有$7$个杯子时，每个杯子都要翻转奇数次才能杯口朝上，$7$个奇数的和为奇数。而每次翻转$4$个杯子，设翻转次数为$n$，那么总的翻转次数为$4n$，$4n$一定是偶数。所以按照每次翻转$4$个杯子的方式，不可能使$7$个杯子的杯口都朝上。
- 当有$10$个杯子时，我们可以通过实际操作来实现杯口全部朝上。将$10$个杯子编号为$1 - 10$。第一次翻转$1 - 4$号杯子；第二次翻转$4 - 7$号杯子；第三次翻转$4$、$8 - 10$号杯子，这样经过$3$次翻转后$10$个杯子的杯口就全部朝上了。
【答案】：因为$7$个杯子每个都要翻转奇数次，$7$个奇数的和是奇数，而每次翻转$4$个杯子，翻转总次数是偶数，所以不能使杯口都朝上；$10$个杯子可以通过合理安排每次翻转的杯子，经过$3$次翻转使杯口全部朝上。