21. 汽车甲做直线运动,前一半时间的平均速度为$9.0m/s$,后一半时间的平均速度为$6.0m/s$,则甲车在这段时间内的平均速度为____$m/s$。汽车乙也做直线运动,前一半路程的平均速度为$3.0m/s$,后一半路程的平均速度为$7.0m/s$,则乙车在这段路程内的平均速度为____$m/s$。
答案:
7.5 4.2 解析:设汽车甲运动前一半时间为t,则后一半时间也为t,甲车前一半时间通过的路程$s_{1}=v_{1}t$,后一半时间通过的路程$s_{2}=v_{2}t$,甲车在这段时间内的平均速度$v_{甲}=\frac{s_{总}}{t_{总}}=\frac{s_{1}+s_{2}}{t + t}=\frac{v_{1}t + v_{2}t}{2t}=\frac{v_{1}+v_{2}}{2}=\frac{9.0m/s + 6.0m/s}{2}=7.5m/s$;设汽车乙运动前一半路程为s,则后一半路程也为s,乙车通过前一半路程所需时间$t_{1}=\frac{s}{v_{乙1}}$,通过后一半路程所需时间$t_{2}=\frac{s}{v_{乙2}}$,则乙车在这段路程内的平均速度$v_{乙}=\frac{s_{总}'}{t_{总}'}=\frac{s + s}{t_{1}+t_{2}}=\frac{2s}{\frac{s}{v_{乙1}}+\frac{s}{v_{乙2}}}=\frac{2v_{乙1}v_{乙2}}{v_{乙1}+v_{乙2}}=\frac{2×3.0m/s×7.0m/s}{3.0m/s + 7.0m/s}=4.2m/s$.
22. 甲、乙、丙三位同学在平直的路面上同向运动,他们运动的图像如图a、b所示。由图b可知,丙同学做____(选填“匀速”或“变速”)直线运动。由图a可判断,甲、乙两同学中,____同学运动快;$A$点为两图线的交点,它表示____;$6s$末时甲、乙两同学相距____$m$。
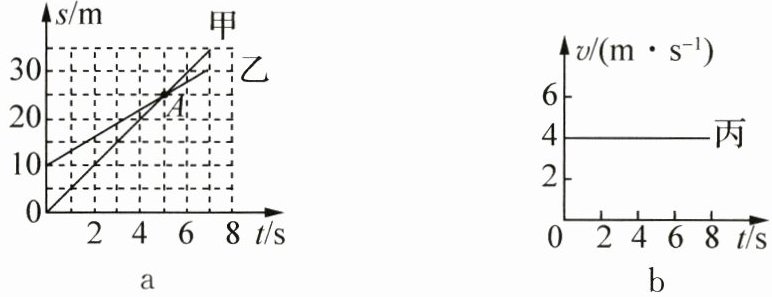
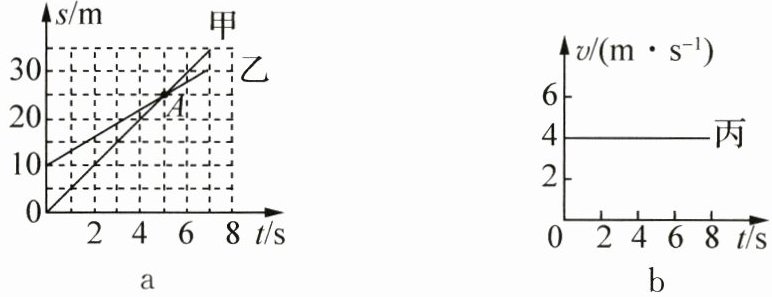
答案:
匀速 甲 甲、乙两同学相遇 2 解析:由图b可知,丙同学的速度为4m/s不变,则丙同学做匀速直线运动。由图a可知,甲、乙均做匀速直线运动,在0~5s内,甲同学运动的距离$s_{甲}=25m$、乙同学运动的距离$s_{乙}=25m - 10m = 15m$,则甲同学的速度$v_{甲}=\frac{s_{甲}}{t}=\frac{25m}{5s}=5m/s$、乙同学的速度$v_{乙}=\frac{s_{乙}}{t}=\frac{15m}{5s}=3m/s$,$v_{甲}>v_{乙}$,所以甲同学运动快;甲、乙两同学在平直的路面上同向运动,开始运动时,乙同学从距离甲出发点10m处出发,A点时甲、乙均在距离甲出发点25m处,则A点表示甲、乙两同学相遇;6s末时,甲通过的路程$s_{甲}'=30m$,乙通过的路程$s_{乙}'=s_{0}+v_{乙}t_{乙}'=10m + 3m/s×6s = 28m$,则6s末时甲、乙两同学相距$\Delta s=s_{甲}'-s_{乙}'=30m - 28m = 2m$.
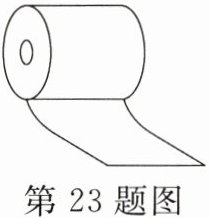
23. 新素养 科学思维 (6分)常用的卷筒纸是紧密地绕成筒状的,如图所示,小明同学想在不把纸拉开的前提下,测量整卷纸的长度。他设计的方案如下。
(1)将同类纸紧密折叠$n$层,用刻度尺测得总厚度为$d$,则单层纸的厚度为____。设纸的宽度为$s$,整卷纸的长度为$L$,则纸筒的体积可表示为$V= $____。
(2)用刻度尺测得纸筒的外半径为$R$,内半径为$r$,则纸筒的体积可表示为____。
(3)由以上两式可得,整卷纸的长度可表示为$L= $____。
(1)将同类纸紧密折叠$n$层,用刻度尺测得总厚度为$d$,则单层纸的厚度为____。设纸的宽度为$s$,整卷纸的长度为$L$,则纸筒的体积可表示为$V= $____。
(2)用刻度尺测得纸筒的外半径为$R$,内半径为$r$,则纸筒的体积可表示为____。
(3)由以上两式可得,整卷纸的长度可表示为$L= $____。

答案:
(1)$\frac{d}{n}$ $\frac{Lsd}{n}$
(2)$\pi s(R^{2}-r^{2})$
(3)$\frac{n\pi(R^{2}-r^{2})}{d}$ 解析:
(1)同类纸折叠n层,用刻度尺测得总厚度为d,则单层纸的厚度为$\frac{d}{n}$;纸的宽度为s,整卷纸的长度为L,则纸筒的体积可表示为$V=\frac{Lsd}{n}$。
(2)不能把纸拉直再测量长度,但卷成筒状的纸的横截面积是由纸的厚度和长度叠加而成的,则测出其横截面积为$\pi(R^{2}-r^{2})$,所以纸筒的体积$V=\pi s(R^{2}-r^{2})$。
(3)由题意可得,$\frac{Lsd}{n}=\pi s(R^{2}-r^{2})$,所以整卷纸长度的表达式为$L=\frac{n\pi(R^{2}-r^{2})}{d}$。
(1)$\frac{d}{n}$ $\frac{Lsd}{n}$
(2)$\pi s(R^{2}-r^{2})$
(3)$\frac{n\pi(R^{2}-r^{2})}{d}$ 解析:
(1)同类纸折叠n层,用刻度尺测得总厚度为d,则单层纸的厚度为$\frac{d}{n}$;纸的宽度为s,整卷纸的长度为L,则纸筒的体积可表示为$V=\frac{Lsd}{n}$。
(2)不能把纸拉直再测量长度,但卷成筒状的纸的横截面积是由纸的厚度和长度叠加而成的,则测出其横截面积为$\pi(R^{2}-r^{2})$,所以纸筒的体积$V=\pi s(R^{2}-r^{2})$。
(3)由题意可得,$\frac{Lsd}{n}=\pi s(R^{2}-r^{2})$,所以整卷纸长度的表达式为$L=\frac{n\pi(R^{2}-r^{2})}{d}$。
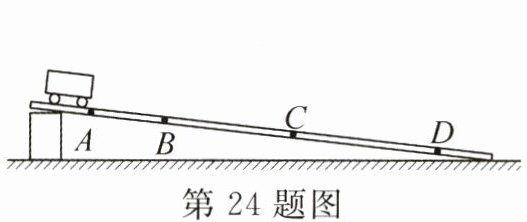
24.(10分)(2025·贵州贵阳期中)小车沿斜面下滑时,在中间一段路程内速度是否变化?如何变化呢?为了探究这个问题,小明选择了长木板、小木块、小车、秒表、记号笔和刻度尺等器材进行探究。
(1)把长木板置于水平桌面上,其左端垫上小木块,在长木板上标记$A$、$B$、$C和D$点,再将小车置于斜面顶端,如图所示。由静止释放小车,发现小车运动过快,不便于记录小车下滑的时间。你认为可以采取的操作是____。
(2)研究长木板中间$BD$段小车运动情况,先用____测量出$BC和CD$的长度,然后再测量小车从$A点由静止运动到B点所用的时间t_{1}$,再次把小车放置于$A点仍由静止运动到C$点,记录所用时间$t_{2}$。小车每次都要从$A$点静止释放的目的是____。
(3)若$BC段的长度为s_{1}$,则$BC段的平均速度v_{BC}= $____(请用所测物理量表示)。
(4)重复上述步骤测量出$CD段的平均速度大于BC$段的平均速度,由此可以得出的初步结论是:小车在$BD$段下滑过程中,速度会变化,而且越来越____。
(1)把长木板置于水平桌面上,其左端垫上小木块,在长木板上标记$A$、$B$、$C和D$点,再将小车置于斜面顶端,如图所示。由静止释放小车,发现小车运动过快,不便于记录小车下滑的时间。你认为可以采取的操作是____。
(2)研究长木板中间$BD$段小车运动情况,先用____测量出$BC和CD$的长度,然后再测量小车从$A点由静止运动到B点所用的时间t_{1}$,再次把小车放置于$A点仍由静止运动到C$点,记录所用时间$t_{2}$。小车每次都要从$A$点静止释放的目的是____。
(3)若$BC段的长度为s_{1}$,则$BC段的平均速度v_{BC}= $____(请用所测物理量表示)。
(4)重复上述步骤测量出$CD段的平均速度大于BC$段的平均速度,由此可以得出的初步结论是:小车在$BD$段下滑过程中,速度会变化,而且越来越____。

答案:
(1)将小木块向左移动合适距离
(2)刻度尺 保证小车每次的运动情况相同
(3)$\frac{s_{1}}{t_{2}-t_{1}}$
(4)大 解析:
(1)若要方便计时,应使斜面的坡度小一些,可将小木块向左移动合适距离,使小车在斜面上通过的时间更长,便于测量时间。
(2)需要测量出BC和CD的长度,测量长度的工具为刻度尺。小车每次都要从A点静止释放的目的是保证小车每次的运动情况相同。
(3)已知小车从A点由静止运动到B点所用的时间$t_{1}$,再次把小车放置于A点仍由静止运动到C点,记录所用时间$t_{2}$,则小车通过BC段所用时间$t_{BC}=t_{2}-t_{1}$,若BC段的长度为$s_{1}$,则BC段的平均速度$v_{BC}=\frac{s_{BC}}{t_{BC}}=\frac{s_{1}}{t_{2}-t_{1}}$。
(4)测量出CD段的平均速度大于BC段的平均速度,说明小车在做加速运动,由此可以得出的初步结论是:小车在BD段下滑过程中,速度会变化,而且越来越大。
(1)将小木块向左移动合适距离
(2)刻度尺 保证小车每次的运动情况相同
(3)$\frac{s_{1}}{t_{2}-t_{1}}$
(4)大 解析:
(1)若要方便计时,应使斜面的坡度小一些,可将小木块向左移动合适距离,使小车在斜面上通过的时间更长,便于测量时间。
(2)需要测量出BC和CD的长度,测量长度的工具为刻度尺。小车每次都要从A点静止释放的目的是保证小车每次的运动情况相同。
(3)已知小车从A点由静止运动到B点所用的时间$t_{1}$,再次把小车放置于A点仍由静止运动到C点,记录所用时间$t_{2}$,则小车通过BC段所用时间$t_{BC}=t_{2}-t_{1}$,若BC段的长度为$s_{1}$,则BC段的平均速度$v_{BC}=\frac{s_{BC}}{t_{BC}}=\frac{s_{1}}{t_{2}-t_{1}}$。
(4)测量出CD段的平均速度大于BC段的平均速度,说明小车在做加速运动,由此可以得出的初步结论是:小车在BD段下滑过程中,速度会变化,而且越来越大。
查看更多完整答案,请扫码查看


