2025年时习之暑假衔接八年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接八年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
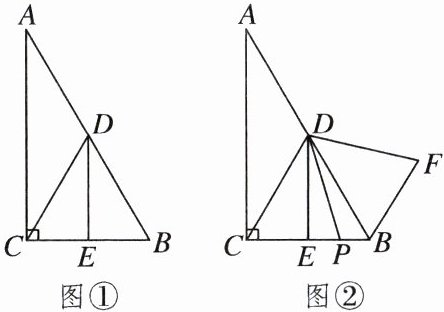
24. (12分)在 $ \mathrm { Rt } \triangle A B C $ 中,$ \angle A C B = 90 ^ { \circ } $,$ \angle A = 30 ^ { \circ } $,点D是AB的中点,点E是CB的中点,连接CD.
(1) 如图①,DE与BC的数量关系是 $ D E = $______BC;
(2) 如图②,若点P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转 $ 60 ^ { \circ } $,得到线段DF,连接BF,请猜想DE,BF,BP三者之间的数量关系,并证明你的结论.
(1) 如图①,DE与BC的数量关系是 $ D E = $______BC;
(2) 如图②,若点P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转 $ 60 ^ { \circ } $,得到线段DF,连接BF,请猜想DE,BF,BP三者之间的数量关系,并证明你的结论.

答案:
(1) $\frac{\sqrt{3}}{2}$
(2) $BF + BP = \frac{2\sqrt{3}}{3}DE$. 理由如下:$\because$ 线段 $DP$ 绕点 $D$ 逆时针旋转 $60^\circ$ 得到线段 $DF$,$\therefore \angle PDF = 60^\circ$,$DP = DF$. $\because$ 点 $D$,$E$ 分别是 $AB$,$CB$ 的中点,$\therefore DE // AC$. $\therefore \angle DEB = \angle ACB = 90^\circ$,即 $DE \perp BC$. $\because$ 点 $E$ 为 $BC$ 的中点,$\therefore CD = DB$. $\because \angle ABC = 90^\circ - \angle A = 60^\circ$,$\therefore \triangle CDB$ 是等边三角形. $\therefore \angle CDB = 60^\circ$. $\therefore \angle CDB - \angle PDB = \angle PDF - \angle PDB$. $\therefore \angle CDP = \angle BDF$. 在 $\triangle DCP$ 和 $\triangle DBF$ 中,$\begin{cases} DC = DB, \\ \angle CDP = \angle BDF, \\ DP = DF, \end{cases} $ $\therefore \triangle DCP \cong \triangle DBF$(SAS),$\therefore CP = BF$. 而 $CP = BC - BP$,$\therefore BF + BP = BC$. $\because DE = \frac{\sqrt{3}}{2}BC$,$\therefore BC = \frac{2\sqrt{3}}{3}DE$. $\therefore BF + BP = \frac{2\sqrt{3}}{3}DE$.
(1) $\frac{\sqrt{3}}{2}$
(2) $BF + BP = \frac{2\sqrt{3}}{3}DE$. 理由如下:$\because$ 线段 $DP$ 绕点 $D$ 逆时针旋转 $60^\circ$ 得到线段 $DF$,$\therefore \angle PDF = 60^\circ$,$DP = DF$. $\because$ 点 $D$,$E$ 分别是 $AB$,$CB$ 的中点,$\therefore DE // AC$. $\therefore \angle DEB = \angle ACB = 90^\circ$,即 $DE \perp BC$. $\because$ 点 $E$ 为 $BC$ 的中点,$\therefore CD = DB$. $\because \angle ABC = 90^\circ - \angle A = 60^\circ$,$\therefore \triangle CDB$ 是等边三角形. $\therefore \angle CDB = 60^\circ$. $\therefore \angle CDB - \angle PDB = \angle PDF - \angle PDB$. $\therefore \angle CDP = \angle BDF$. 在 $\triangle DCP$ 和 $\triangle DBF$ 中,$\begin{cases} DC = DB, \\ \angle CDP = \angle BDF, \\ DP = DF, \end{cases} $ $\therefore \triangle DCP \cong \triangle DBF$(SAS),$\therefore CP = BF$. 而 $CP = BC - BP$,$\therefore BF + BP = BC$. $\because DE = \frac{\sqrt{3}}{2}BC$,$\therefore BC = \frac{2\sqrt{3}}{3}DE$. $\therefore BF + BP = \frac{2\sqrt{3}}{3}DE$.
查看更多完整答案,请扫码查看


