第46页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1. 用一块直角三角尺确定一个圆的圆心的位置,至少要用 (
A.1次
B.2次
C.3次
D.4次
B
)A.1次
B.2次
C.3次
D.4次
答案:
1. B
2. 如图,经过原点的$\odot P$与x轴、y轴分别交于A、B两点,C是$\widehat {OB}$上一点,则$∠C$的度数为 (

A.$80^{\circ }$
B.$90^{\circ }$
C.$100^{\circ }$
D.无法确定
B
)
A.$80^{\circ }$
B.$90^{\circ }$
C.$100^{\circ }$
D.无法确定
答案:
2. B
3. (新情境·现实生活)一块圆形玻璃镜面损坏了一部分,为了得到同样大小的镜面,工人师傅用直角尺作如图所示的测量,测得$AB=12cm,BC=5cm$,则圆形玻璃镜面的半径为

$\frac{13}{2}$
cm.
答案:
3. $\frac{13}{2}$
4. (2024·宜宾)如图,AB是$\odot O$的直径,若$∠CDB=60^{\circ }$,则$∠ABC$的度数为

$30^{\circ}$
.
答案:
4. $30^{\circ}$
5. 如图,$△ABC$内接于一圆,$∠CAB=30^{\circ },∠B=60^{\circ }$,O是AB的中点,$CD⊥AB$于点E,交圆于点D.
(1) 求证:点O是圆心;
(2) 求$∠DAE$的度数.

(1) 求证:点O是圆心;
(2) 求$∠DAE$的度数.

答案:
5.
(1) $\because \angle CAB = 30^{\circ}, \angle B = 60^{\circ}, \therefore \angle ACB = 180^{\circ} - \angle CAB - \angle B = 90^{\circ}$. 又 $\because A$、$B$ 两点都在圆上, $\therefore AB$ 是圆的直径. 又 $\because O$ 是 $AB$ 的中点, $\therefore$ 点 $O$ 是圆心
(2) $\because \overgroup{AC} = \overgroup{AC}, \therefore \angle D = \angle B = 60^{\circ}. \because AB \perp CD, \therefore \angle DAE = 90^{\circ} - \angle D = 30^{\circ}$
(1) $\because \angle CAB = 30^{\circ}, \angle B = 60^{\circ}, \therefore \angle ACB = 180^{\circ} - \angle CAB - \angle B = 90^{\circ}$. 又 $\because A$、$B$ 两点都在圆上, $\therefore AB$ 是圆的直径. 又 $\because O$ 是 $AB$ 的中点, $\therefore$ 点 $O$ 是圆心
(2) $\because \overgroup{AC} = \overgroup{AC}, \therefore \angle D = \angle B = 60^{\circ}. \because AB \perp CD, \therefore \angle DAE = 90^{\circ} - \angle D = 30^{\circ}$
6. 如图,$□ ABCD$的顶点A、B、D在$\odot O$上,顶点C在$\odot O$的直径BE上,连接AE,$∠E=36^{\circ }$,则$∠ADC$的度数是 (

A.$44^{\circ }$
B.$54^{\circ }$
C.$72^{\circ }$
D.$53^{\circ }$
B
)
A.$44^{\circ }$
B.$54^{\circ }$
C.$72^{\circ }$
D.$53^{\circ }$
答案:
6. B
7. 如图,$\widehat {AC}$、$\widehat {BD}$皆为半圆,$\widehat {AC}$与$\widehat {BD}$相交于E点,其中A、B、C、D在同一条直线上,且B为AC的中点.若$\widehat {CE}$的度数为$58^{\circ }$,则$\widehat {BE}$的度数为 (
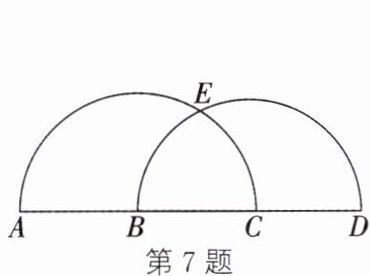
A.$58^{\circ }$
B.$60^{\circ }$
C.$62^{\circ }$
D.$64^{\circ }$
D
)
A.$58^{\circ }$
B.$60^{\circ }$
C.$62^{\circ }$
D.$64^{\circ }$
答案:
7. D 解析: 如图, 连接 $BE$、$DE$. 由题意, 得 $AC$ 是左边半圆的直径, $BD$ 是右边半圆的直径. $\because B$ 为 $AC$ 的中点, $\therefore$ 点 $B$ 是左边半圆的圆心. $\because \overgroup{CE}$ 的度数为 $58^{\circ}, \therefore \angle EBC = 58^{\circ}. \because BD$ 是右边半圆的直径, $\therefore \angle BED = 90^{\circ}, \therefore$ 在 $Rt \triangle BED$ 中, $\angle EDB = 90^{\circ} - 58^{\circ} = 32^{\circ}, \therefore \overgroup{BE}$ 的度数为 $32^{\circ} × 2 = 64^{\circ}$.

7. D 解析: 如图, 连接 $BE$、$DE$. 由题意, 得 $AC$ 是左边半圆的直径, $BD$ 是右边半圆的直径. $\because B$ 为 $AC$ 的中点, $\therefore$ 点 $B$ 是左边半圆的圆心. $\because \overgroup{CE}$ 的度数为 $58^{\circ}, \therefore \angle EBC = 58^{\circ}. \because BD$ 是右边半圆的直径, $\therefore \angle BED = 90^{\circ}, \therefore$ 在 $Rt \triangle BED$ 中, $\angle EDB = 90^{\circ} - 58^{\circ} = 32^{\circ}, \therefore \overgroup{BE}$ 的度数为 $32^{\circ} × 2 = 64^{\circ}$.

查看更多完整答案,请扫码查看


