《2025年通城学典课时作业本九年级数学上册苏科版江苏专版》

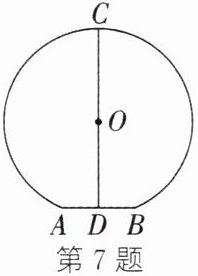
7. (新情境·现实生活)(2024·通辽)如图,圆形拱门最下端AB在地面上,D为AB的中点,C为拱门最高点,线段CD经过拱门所在圆的圆心. 若$AB=1m,CD=2.5m$,则拱门所在圆的半径为 (B)

A.1.25 m
B.1.3 m
C.1.4 m
D.1.45 m

答案： 7. B 解析：连接$ OA $、$ OB $。$ \because OA = OB $，$ D $为$ AB $的中点，$ \therefore CD \perp AB $，$ AD = \frac { 1 } { 2 } AB = 0.5 \mathrm { m } $。设拱门所在圆的半径为$ r \mathrm { m } $，则$ OA = OC = r \mathrm { m } $，$ OD = ( 2.5 - r ) \mathrm { m } $。在$ \mathrm { Rt } \triangle ADO $中，由勾股定理，得$ OA ^ { 2 } = AD ^ { 2 } + OD ^ { 2 } $，即$ r ^ { 2 } = 0.5 ^ { 2 } + ( 2.5 - r ) ^ { 2 } $，解得$ r = 1.3 $，$ \therefore $拱门所在圆的半径为$ 1.3 \mathrm { m } $。

8. 在平面直角坐标系中,以点$(3,0)$为圆心,5为半径作圆,则该圆与y轴的交点的坐标为$ ( 0,4 ) $、$ ( 0 , - 4 ) $.

答案： 8. $ ( 0,4 ) $、$ ( 0 , - 4 ) $

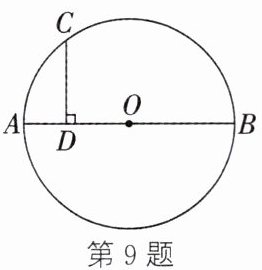
9. 如图,AB是$\odot O$的直径,点C在$\odot O$上,$CD⊥AB$于点D. 已知$CD=4,AD=2$,则$\odot O$的半径为5.

答案： 9. 5 解析：连接$ OC $。设$ \odot O $的半径为$ r $，则$ OC = r $，$ OD = OA - AD = r - 2 $。在$ \mathrm { Rt } \triangle CDO $中，$ OC ^ { 2 } = CD ^ { 2 } + OD ^ { 2 } $，即$ r ^ { 2 } = 4 ^ { 2 } + ( r - 2 ) ^ { 2 } $，解得$ r = 5 $。$ \therefore \odot O $的半径为5。

10. 如图,过A、C、D三点的圆的圆心为点E,过B、F、E三点的圆的圆心为点D. 如果$∠A=63^{\circ }$,那么$∠B=$18$^{\circ }$.

答案：
10. 18 解析：如图，连接$ CE $、$ DE $。$ \because DE = BD $，$ \therefore \angle 2 = \angle B $。同理，可得$ \angle 5 = \angle 6 $，$ \angle 3 = \angle A = 63 ^ { \circ } $。$ \because \angle 6 = \angle 2 + \angle B = 2 \angle B $，$ \angle CEB = \angle A + \angle 3 = 126 ^ { \circ } $，$ \therefore \angle 1 = 180 ^ { \circ } - \angle 5 - \angle 6 = 180 ^ { \circ } - 4 \angle B $，$ \therefore \angle CEB = \angle 1 + \angle 2 = 180 ^ { \circ } - 3 \angle B = 126 ^ { \circ } $，$ \therefore \angle B = 18 ^ { \circ } $。

11. 如图,AC是$\odot O$的直径,点B在$\odot O$上(不与点A、C重合),点D在AC的延长线上,连接BD交$\odot O$于点E,$∠AOB=3∠D$. 求证:$DE=OB$.

答案：
11. 如图，连接$ OE $。设$ \angle D = x $。$ \because OB = OE $，$ \therefore \angle B = \angle OEB $。$ \because \angle OEB $是$ \triangle DEO $的外角，$ \therefore \angle OEB = \angle D + \angle DOE = x + \angle DOE $。$ \because \angle AOB $是$ \triangle BOD $的外角，$ \therefore \angle AOB = \angle B + \angle D = \angle OEB + \angle D = x + \angle DOE + x = \angle DOE + 2 x $。$ \because \angle AOB = 3 \angle D = 3 x $，$ \therefore \angle DOE + 2 x = 3 x $，即$ \angle DOE = x = \angle D $，$ \therefore DE = OE $，$ \therefore DE = OB $

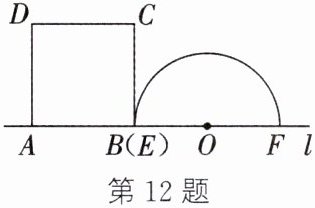
12. 如图,矩形ABCD与以EF为直径的半圆O在直线l的上方,线段AB与点E、F都在直线l上,且$AB=7,EF=10,BC＞5$. 点B从点E处出发,沿射线EF的方向运动,矩形ABCD随之运动. 在点B运动的过程中,当AD、BC都与半圆O相交时,设这两个交点为G、H,连接OG、OH. 若$∠GOH$为直角,求此时BE的长.

答案：
12. 如图。设$ BE = t $。$ \because EF = 10 $，$ \therefore OE = OG = OH = 5 $。$ \because \angle GOH = 90 ^ { \circ } $，$ \therefore \angle AOG + \angle BOH = 90 ^ { \circ } $。$ \because $在矩形$ ABCD $中，$ \angle DAB = \angle ABC = 90 ^ { \circ } $，$ \therefore \angle AGO + \angle AOG = 90 ^ { \circ } $，$ \therefore \angle AGO = \angle BOH $。在$ \triangle GAO $和$ \triangle OBH $中，$ \begin{cases} \angle GAO = \angle OBH = 90 ^ { \circ } \\ \angle AGO = \angle BOH \\ OG = HO \end{cases} $ $ \therefore \triangle GAO \cong \triangle OBH $，$ \therefore GA = OB = BE - OE = t - 5 $。$ \because AB = 7 $，$ \therefore AE = BE - AB = t - 7 $，$ \therefore AO = OE - AE = 5 - ( t - 7 ) = 12 - t $。在$ \mathrm { Rt } \triangle GAO $中，由勾股定理，得$ AG ^ { 2 } + AO ^ { 2 } = OG ^ { 2 } $，$ \therefore ( t - 5 ) ^ { 2 } + ( 12 - t ) ^ { 2 } = 5 ^ { 2 } $，即$ t ^ { 2 } - 17 t + 72 = 0 $，解得$ t _ { 1 } = 8 $，$ t _ { 2 } = 9 $，$ \therefore BE $的长为8或9