《2025年黄冈金牌之路练闯考六年级数学下册北师大版》

1.填空。(主要对应目标:6106)
　(1)一个圆柱和一个圆锥等底等高，如果圆柱的体积是27dm³,那么圆锥的体积是(　　　)dm³。如果圆锥的体积是6dm³,那么圆柱的体积是(　　　)dm³。
　(2)把一个圆柱削成一个最大的圆锥,削去部分的体积是24cm³，这个圆锥的体积是(　　　)cm³。
　(3)一堆沙子近似于圆锥形,体积是39.25m³，底面半径是5m,高是(　　　)m。

答案：
(1)9　18　
(2)12　
(3)1.5

2.计算下面各圆锥的体积。(主要对应目标:6106)
　
　(2)
　　

答案：
(1)$\frac{1}{3}$×7×4.8 = 11.2(cm³)　
(2)$\frac{1}{3}$×3.14×(8÷2)²×15 = 251.2(dm³)

　(1)(湖南郴州)圆锥的高不变,底面半径扩大到原来的3倍，则它的体积扩大到原来的(　　　)倍。
A.3　　　　B.6　　　　C.9　　　　D.27

答案：
(1)C　

　(2)如图，圆柱形容器底面积和圆锥形杯子口的面积相等。将圆柱形容器里的橙汁倒入圆锥形杯子中,可以倒满(　　　)杯。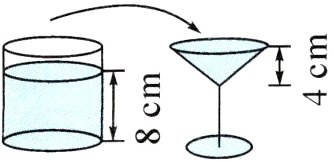
A.2
B.3　　　　　　　　　　　
C.4
D.6

答案：
(2)D

4.把冰淇淋的上面部分看作是近似的圆锥，这个冰淇淋的体积是多少？(单位:cm)(主要对应目标:6106)
　

答案： $\frac{1}{3}$×3.14×(4÷2)²×6 = 25.12(cm³)　$\frac{1}{3}$×3.14×(4÷2)²×12 = 50.24(cm³)25.12 + 50.24 = 75.36(cm³)

5.(江西赣州)一个圆锥形沙堆的底面积是28.26m²,高是2m。用这堆沙在10m宽的公路上铺2cm厚的路面，能铺多少米？(主要对应目标:6106)

答案： 2cm = 0.02m 　28.26×2×$\frac{1}{3}$÷(10×0.02) = 94.2(m)

6.一个底面直径是6cm的圆锥，从顶点沿着它的高将它切成两半后，表面积增加了48cm²。这个圆锥的体积是多少立方厘米？(主要对应目标:6106)

答案： 48÷2×2÷6 = 8(cm)　$\frac{1}{3}$×3.14×(6÷2)²×8 = 75.36(cm³)