《2025年黄冈金牌之路练闯考六年级数学下册北师大版》

1.填空。
　(1)食堂运进at大米,每天用去nt,用了10天,a−10n表示(　　　　　　　　　　　)。
　(2)一列高铁从广州驶向武汉,每时行ykm,行驶2时后距离武汉xkm,这列高铁到武汉还要(　　　　　　)时，从广州到武汉的路程一共有(　　　　　)km。
　(3)鞋的尺码通常用“码”或“厘米”作单位，它们之间的换算关系是b = 2a−10(b表示码数，a表示脚长)。小哲今年的脚长22cm,他要穿(　　　)码的鞋;小哲要穿40码的鞋的时候，他的脚长(　　　)cm。

答案：
(1)剩下的大米质量与已吃的大米质量的比是2:1。
(2)$\frac{x}{y}=2$，则$y + 2x$。
(3)34，2。

　(1)(广西南宁)一件大衣先打八折销售，再降价y元。现在的价格是x元,这件大衣的原价是(　　　)元。
A.x÷80% + y　　　　B.(x + y)×80%
C.80%y + x　　　　　D.(x + y)÷80%

答案：
(1)D

　(2)一辆汽车在一条公路上行驶,已经行驶了全长的$\frac{1}{3}$，离中点还有5km，求这条公路有多长。如果设这条公路的全长是xkm，那么列式正确的是(　　　)。
A.x - $\frac{1}{3}$x = 5　　　　　B.$\frac{1}{2}$x - $\frac{1}{3}$x = 5
C.$\frac{1}{3}$x = 5　　　　　　　D.$\frac{1}{2}$x = 5

答案：
(2)B

　(3)(浙江宁波)下面数量关系不能用方程“$\frac{1}{3}$x + x = 40”来表示的是(　　　)。
　　
　　

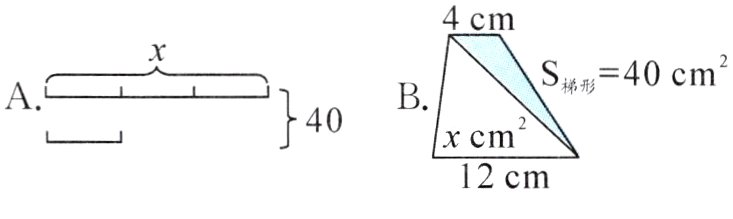
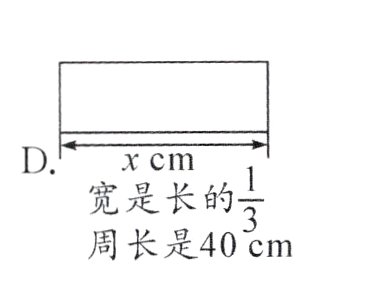
答案：
(3)D

3.列方程解决问题。
　　(1)(山西太原)小林和小军沿着公园的环湖跑道跑步,跑道一圈的长度是4500m。他们两人同时从同一地点反向跑步，如图所示。
　　　　小林每分跑170m,小军每分跑130m,多长时间后两人相遇？
　
　　(2)某自然保护区里鹤和龟的数量一共有28只,两种动物的腿一共有84条。鹤和龟各有多少只？

答案：
(1)解：设x分后两人相遇。(170 + 130)x = 4500，x = 15。
(2)解：设鹤有x只，则龟有(28 - x)只。2x + 4(28 - x) = 84，x = 14，28 - x = 28 - 14 = 14。

4.商店购进了一批钢笔，决定以每支9元的价格出售。第一周卖出了60%，这时还差72元收回全部成本,又过了一周后全部售出，总共获得利润288元。这批钢笔一共有多少支？(列方程解答)

答案： 解：设这批钢笔一共有x支。9×60%x + 72 = 9x - 288，x = 100。