《2025年课时训练八年级数学下册人教版江苏人民出版社》

10（2023·重庆中考）如图，在正方形 ABCD 中，O 为对角线 AC 的中点，E 为正方形内一点，连接 BE，BE＝BA，连接 CE 并延长，与∠ABE 的平分线交于点 F，连接 OF，若 AB＝2，则 OF 的长度为( )．


A. 2
B. $\sqrt{3}$
C. 1
D. $\sqrt{2}$

答案： D

11（2023·枣庄中考）如图，在正方形 ABCD 中，对角线 AC 与 BD 相交于点 O，E 为 BC 上一点，CE＝7，F 为 DE 的中点，若△CEF 的周长为 32，则 OF 的长为_______．

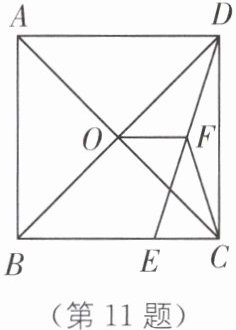
答案： $\frac{17}{2}$

12（2023·天津中考）如图，在边长为 3 的正方形 ABCD 的外侧，作等腰三角形 ADE，EA＝ED＝$\frac{5}{2}$．
（1）△ADE 的面积为_______；
（2）若 F 为 BE 的中点，连接 AF 并延长，与 CD 相交于点 G，则 AG 的长为_______．

答案： 3@@$\sqrt{13}$

13 已知在线段 AB 上有一点 C（点 C 不与 A，B 重合且 AC＞BC），分别以 AC，BC 为边作正方形 ACED 和正方形 BCFG，其中点 F 在边 CE 上，连接 AG.

（1）如图（1），若 AC＝7，BC＝5，则 AG＝_______；
（2）如图（2），若点 C 是线段 AB 的三等分点，连接 AE，EG，求证：△AEG 是直角三角形.

答案： 13.（1）13 （2）设\(BC = a(a\gt0)\)，
∵四边形ACED和四边形BCFG都是正方形， 点C是线段AB的三等分点，
∴\(AC = CE = 2BC = 2CF = 2a\)， \(BC = BG = FG = CF = EF = a\)， \(\angle B=\angle ACE=\angle EFG = 90^{\circ}\)，
∴\(AE^{2}=AC^{2}+CE^{2}=8a^{2}\)，\(AB = 3BC = 3a\)， \(AG^{2}=AB^{2}+BG^{2}=9a^{2}+a^{2}=10a^{2}\)， \(EG^{2}=EF^{2}+FG^{2}=a^{2}+a^{2}=2a^{2}\)，
∴\(AE^{2}+EG^{2}=8a^{2}+2a^{2}=10a^{2}\).
∴\(AG^{2}=AE^{2}+EG^{2}\).
∴\(\triangle AEG\)是直角三角形. 

14 如图，四边形 ABCD 是正方形，E 是 BC 边所在直线上的点，∠AEF＝90°，且 EF 交正方形外角∠DCG 的平分线 CF 于点 F.
（1）当点 E 是线段 BC 中点时（如图（1）），易证 AE＝EF，不需证明.
（2）当点 E 在线段 BC 上（如图（2））或在线段 BC 延长线上（如图（3））时，（1）中的结论是否仍然成立? 请写出你的猜想，并选择图（2）或图（3）的一种结论给予证明.

答案：
14.（2）当点E在线段BC上时，结论\(AE = EF\)仍成立. 理由如下： 如图（1），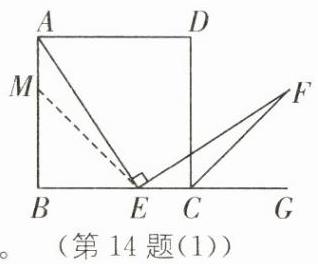
在AB上取一点M，使\(AM = EC\)，连接ME.
∴\(BM = BE\).
∴\(\angle BME = 45^{\circ}\).
∴\(\angle AME = 135^{\circ}\).
∵CF是外角平分线，
∴\(\angle DCF = 45^{\circ}\).
∴\(\angle ECF = 135^{\circ}\).
∴\(\angle AME=\angle ECF\).
∵\(\angle AEB+\angle BAE = 90^{\circ}\)，\(\angle AEB+\angle CEF = 90^{\circ}\)，
∴\(\angle BAE=\angle CEF\).
∴\(\triangle AME\cong\triangle ECF\)（ASA）.
∴\(AE = EF\). 当点E在BC延长线上时，结论\(AE = EF\)仍成立，理由如下： 如图（2），在BA的延长线上取一点N，使\(AN = CE\)，连接NE.
∴\(BN = BE\).
∴\(\angle N=\angle NEC = 45^{\circ}\).
∵CF平分\(\angle DCG\)，
∴\(\angle FCE = 45^{\circ}\).
∴\(\angle N=\angle ECF\).
∵四边形ABCD是正方形，
∴\(AD\parallel BE\).
∴\(\angle DAE=\angle BEA\).
∴\(\angle DAE + 90^{\circ}=\angle BEA + 90^{\circ}\)，即\(\angle NAE=\angle CEF\).
∴\(\triangle ANE\cong\triangle ECF\)（ASA）.
∴\(AE = EF\). [