1. 重力做功等于重力势能的减少,即
重力做功等于重力势能的减少,即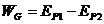
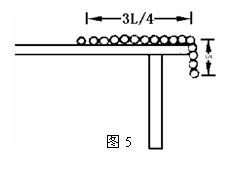
例7.如图5所示,链条的总长度为L,总质量为m,开始时链条有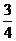 L在光滑水平桌面上,而
L在光滑水平桌面上,而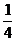 L长度垂在光滑桌边外.若要把链条的悬挂部分拉回桌面,则至少要克服重力做功_______J
L长度垂在光滑桌边外.若要把链条的悬挂部分拉回桌面,则至少要克服重力做功_______J
解析:把链条的悬挂部分拉回桌面,则至少要克服重力做功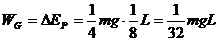
3.恒定功率做功:
如功率恒定时,用公式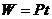 等效替代变力功,是计算变力功的常见方法。
例5.输出功率保持10kW的起重机起吊质量为500kg的静止重物,当重物升高到2m时,速度达到最大,若g取10m/s,则此过程所用时间为多少?
解析:由P=Fv知:起重机的输出功率恒定时,物体速度增大的同时它所提供的拉力是减小的。所以货物速度V最大时F=mg,故 P=mgv
得v=P/mg=2m/s
从起吊到重物速度达到最大的过程中,只有起重机的拉力和重力对物体做功,拉力为变力,其功率恒定,故拉力功可由W=Pt替代,根据动能定理
Pt-mgh=mv2/2得:t=1.1s
4.恒定压强做功:
等效替代变力功,是计算变力功的常见方法。
例5.输出功率保持10kW的起重机起吊质量为500kg的静止重物,当重物升高到2m时,速度达到最大,若g取10m/s,则此过程所用时间为多少?
解析:由P=Fv知:起重机的输出功率恒定时,物体速度增大的同时它所提供的拉力是减小的。所以货物速度V最大时F=mg,故 P=mgv
得v=P/mg=2m/s
从起吊到重物速度达到最大的过程中,只有起重机的拉力和重力对物体做功,拉力为变力,其功率恒定,故拉力功可由W=Pt替代,根据动能定理
Pt-mgh=mv2/2得:t=1.1s
4.恒定压强做功:
对液体、气体做功,若压强恒定,可用公式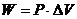 直接计算
直接计算
例6.人的心脏每跳一次大约输送8×10-5 m3的血液,正常人血压(可看做心脏输送血液的压强)的平均值为1.5×104 Pa,心跳约每分钟70次.据此估测心脏工作的平均功率约为_____W.
解析:心跳一次,心脏做功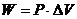 =1.5×104×8×10-5J=1.2J
=1.5×104×8×10-5J=1.2J
则每分钟心脏做功W总=1.2×70=84J
心脏工作的平均功率约为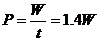
2.3转换为平均作用力求功
如作用于物体的力是变力,且该力随物体位移呈线性变化,则可以求出该变力的平均作用力 ,由
,由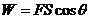 求功,相当于计算恒力功。
求功,相当于计算恒力功。
例4.用质量为5kg的均匀铁索从10m深的井中吊起一质量为20kg的物体,在这个过程中人至少要做多少功?(g取10m/s) 解析:由于拉吊的过程中,铁索的长度逐渐缩短,而其重力不能忽略不计,故人的最小拉力(物体匀速上升时的拉力)也在逐渐减小。由题意可知,该拉力大小与铁索缩短的长度之间的关系为线性关系。
开始拉铁索时,拉力F1=Mg+mg=250N
铁索全部拉完时,拉力F2=Mg=200N
所以人拉力平均值为F=(F1+F2)/2=225N,
力的作用点的位移为10m,
则人拉力做功的最小值W=FS=225×10J=2250J?
2. 2过程转换:物体做曲线运动时的变力功问题,可用微元法将曲线化为直线,把变力功问题转化为恒力做功问题。
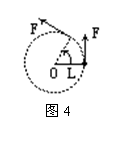
例3. 如图4所示,磨杆长为L,在杆端施以与杆垂直且大小不变的力F。求杆绕轴转动一周,力F做的功。
2过程转换:物体做曲线运动时的变力功问题,可用微元法将曲线化为直线,把变力功问题转化为恒力做功问题。
例3. 如图4所示,磨杆长为L,在杆端施以与杆垂直且大小不变的力F。求杆绕轴转动一周,力F做的功。
解析:磨杆绕轴一周,力的方向始终在变,不能直接用W=FScosα计算。将圆周分成无限个小段,在每一小段弧长可以认为等于对应的弦,且力F的方向不变,可求得元功△W=F·△S,再累加求得杠转一周力F做功W=F·2πL。
2.1对象转换:将变力做功转换为恒力做功,即可应用公式W=FS·cosα求解
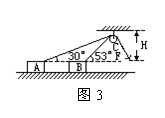 例2. 如图3所示,一个人用恒力F=80牛拉绳子的C端,绳子跨过光滑的定滑轮将一个静止的物体由位置A拉到位置B,图中H=2.0m,求此过程中拉力对物体做的功。
例2. 如图3所示,一个人用恒力F=80牛拉绳子的C端,绳子跨过光滑的定滑轮将一个静止的物体由位置A拉到位置B,图中H=2.0m,求此过程中拉力对物体做的功。
解析: 物体在运动过程中,绳作用在物体上的拉力方向不断变化,属变力做功的问题。如果把力F的作用点C作为做功对象,求绳子拉物体的变力之功便转化为求人拉绳子的恒力之功。
物体由A运动到B的过程中,绳C端位移为:
S=H(1/sin30°-1/sin53°)=1.5m。
1.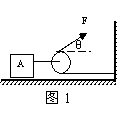 恒力做功:可用公式W=FScosθ直接计算,其中S为力的作用点对地面的位移,θ为力F和位移S之间的夹角。
恒力做功:可用公式W=FScosθ直接计算,其中S为力的作用点对地面的位移,θ为力F和位移S之间的夹角。
例1.一个人通过一个动滑轮用恒力拉动物体A,已知恒力为F,与水平地面夹角为θ,如图,不计绳子的质量和滑轮间的摩擦,当物体A被拉着向右移动了S时,人所做功为( )
A、FS B、2FS
C、FS(1+COSθ) D、无法确定
 解析:本例中求“人所做的功”即人用力F作用在绳的端点P所做的功。由图知,当物体A被拉着向右移动了S时,绳端点P的位移S’=
解析:本例中求“人所做的功”即人用力F作用在绳的端点P所做的功。由图知,当物体A被拉着向右移动了S时,绳端点P的位移S’=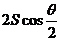 ,力F与S’的夹角为
,力F与S’的夹角为 ,则力F对绳端点P所做的功为
,则力F对绳端点P所做的功为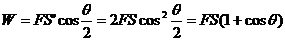 ,答案选D.
,答案选D.
2.已知矩形的两个顶点位于x轴上,另两个顶点位于抛物线y =4-x2在x轴上方的曲线上,求这种矩形中面积最大者的边长.
学习笔记
教师备课
学习笔记
教师备课
学习笔记
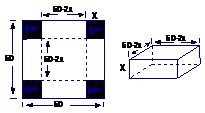
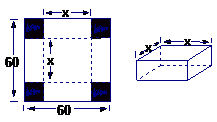 例1在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
例1在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
解法一:设箱底边长为xcm,则箱高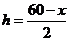 cm,得箱子容积
cm,得箱子容积

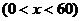 .
.
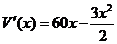
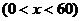 令
令 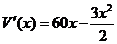 =0,
=0,
解得 x=0(舍去),x=40, 并求得 V(40)=16 000
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
 解法二:设箱高为xcm,则箱底长为(60-2x)cm,则得箱子容积
解法二:设箱高为xcm,则箱底长为(60-2x)cm,则得箱子容积
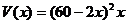
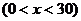 .(后面同解法一,略)
.(后面同解法一,略)
由题意可知,当x过小或过大时箱子容积很小,所以最大值出现在极值点处.事实上,可导函数 、
、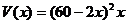 在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值
在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值
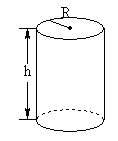
例2圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?
解:设圆柱的高为h,底半径为R,则表面积S=2πRh+2πR2
由V=πR2h,得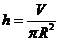 ,则S(R)= 2πR
,则S(R)= 2πR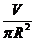 + 2πR2=
+ 2πR2=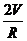 +2πR2
+2πR2
 令
令 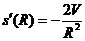 +4πR=0
+4πR=0
解得,R=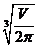 ,
,
从而h=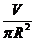 =
= =
=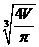 =2
=2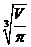
即h=2R, 因为S(R)只有一个极值,所以它是最小值
答:当罐的高与底直径相等时,所用材料最省
变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使所用材料最省?
提示:S=2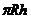 +
+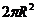
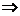 h=
h=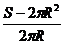
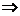 V(R)=
V(R)=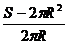
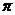 R
R =
=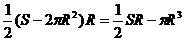
 )=0
)=0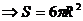
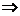
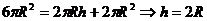 .
.
例3已知某商品生产成本C与产量q的函数关系式为C=100+4q,价格p与产量q的函数关系式为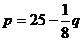 .求产量q为何值时,利润L最大?
.求产量q为何值时,利润L最大?
分析:利润L等于收入R减去成本C,而收入R等于产量乘价格.由此可得出利润L与产量q的函数关系式,再用导数求最大利润.
解:收入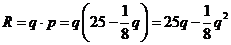 ,
,
利润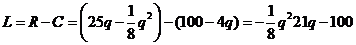
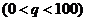
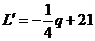 令
令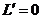 ,即
,即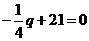 ,
,
求得唯一的极值点

答:产量为84时,利润L最大
课堂巩固:
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
归纳反思:
合作探究
1.某制造商制造并出售球型瓶装的某种饮料.瓶子的制造成本是
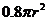 分,其中
分,其中 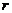 是瓶子的半径,单位是厘米。已知每出售1 mL的饮料,制造商可获利 0.2 分,且制造商能制作的瓶子的最大半径为 6cm
是瓶子的半径,单位是厘米。已知每出售1 mL的饮料,制造商可获利 0.2 分,且制造商能制作的瓶子的最大半径为 6cm
问题:(1)瓶子的半径多大时,能使每瓶饮料的利润最大?
(2)瓶子的半径多大时,每瓶的利润最小?

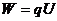 直接计算,既适用于匀强电场的恒力做功,也适用于非匀强电场的变力做功。
直接计算,既适用于匀强电场的恒力做功,也适用于非匀强电场的变力做功。