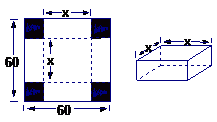
 例1在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
例1在边长为60 cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?
解法一:设箱底边长为xcm,则箱高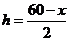 cm,得箱子容积
cm,得箱子容积
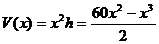
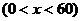 .
.
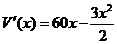
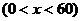 令
令 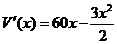 =0,
=0,
解得 x=0(舍去),x=40, 并求得 V(40)=16 000
由题意可知,当x过小(接近0)或过大(接近60)时,箱子容积很小,因此,16 000是最大值
答:当x=40cm时,箱子容积最大,最大容积是16 000cm3
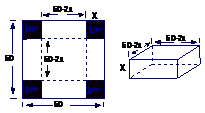 解法二:设箱高为xcm,则箱底长为(60-2x)cm,则得箱子容积
解法二:设箱高为xcm,则箱底长为(60-2x)cm,则得箱子容积
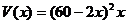
 .(后面同解法一,略)
.(后面同解法一,略)
由题意可知,当x过小或过大时箱子容积很小,所以最大值出现在极值点处.事实上,可导函数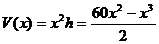 、
、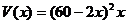 在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值
在各自的定义域中都只有一个极值点,从图象角度理解即只有一个波峰,是单峰的,因而这个极值点就是最值点,不必考虑端点的函数值
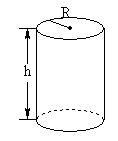
例2圆柱形金属饮料罐的容积一定时,它的高与底与半径应怎样选取,才能使所用的材料最省?
解:设圆柱的高为h,底半径为R,则表面积S=2πRh+2πR2
由V=πR2h,得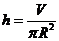 ,则S(R)= 2πR
,则S(R)= 2πR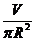 + 2πR2=
+ 2πR2=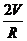 +2πR2
+2πR2
 令
令 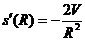 +4πR=0
+4πR=0
解得,R= ,
,
从而h=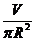 =
= =
=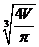 =2
=2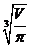
即h=2R, 因为S(R)只有一个极值,所以它是最小值
答:当罐的高与底直径相等时,所用材料最省
变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使所用材料最省?
提示:S=2 +
+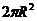
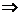 h=
h=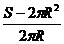
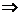 V(R)=
V(R)=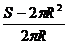
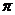 R
R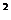 =
=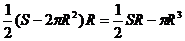
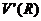 )=0
)=0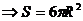
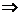
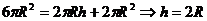 .
.
例3已知某商品生产成本C与产量q的函数关系式为C=100+4q,价格p与产量q的函数关系式为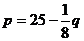 .求产量q为何值时,利润L最大?
.求产量q为何值时,利润L最大?
分析:利润L等于收入R减去成本C,而收入R等于产量乘价格.由此可得出利润L与产量q的函数关系式,再用导数求最大利润.
解:收入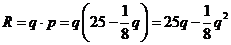 ,
,
利润
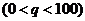
 令
令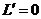 ,即
,即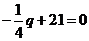 ,
,
求得唯一的极值点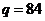

答:产量为84时,利润L最大
课堂巩固:
用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
归纳反思:
合作探究
1.某制造商制造并出售球型瓶装的某种饮料.瓶子的制造成本是
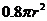 分,其中
分,其中  是瓶子的半径,单位是厘米。已知每出售1 mL的饮料,制造商可获利 0.2 分,且制造商能制作的瓶子的最大半径为 6cm
是瓶子的半径,单位是厘米。已知每出售1 mL的饮料,制造商可获利 0.2 分,且制造商能制作的瓶子的最大半径为 6cm
问题:(1)瓶子的半径多大时,能使每瓶饮料的利润最大?
(2)瓶子的半径多大时,每瓶的利润最小?
- 答案

