1. A. something　　　 　　　　 B. anything　　 　　 C. somebody　 　　　　 D. anybody

如果力F随位移x的变化关系明确，始末位置清楚，可在平面直角坐标系内画出F-S图象，图象下方与坐标轴所围的“面积”表示功。图象求功具有形象、直观、简捷的特点。

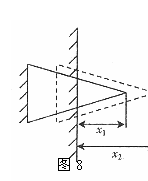
例11. 用铁锤将一铁钉击入木块，设木块对铁钉的阻力与铁钉钉入木块内的深度成正比。在铁锤击第一次时，能把铁钉击入木块内1cm，如图8。问击第二次时，能击入多深？(设铁锤每次做功都相等)

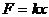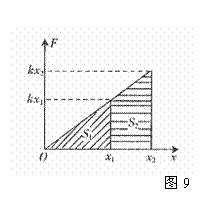
解析：因为阻力，以F为纵坐标，F方向上的位移x为横坐标，作出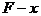图象，如图8所示，函数线与x轴所夹阴影部分面积的值等于F对铁钉做的功。

由于两次做功相等，故有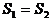：(面积)

即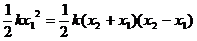

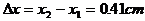
小结：一个看似复杂的变力做功问题，用常规方法无从下手，但通过图象变换，就使得解题过程简单、明了。可见，图象法是一个很好的解题方法，值得掌握。

高中物理"功的计算立体化复习"在我们教学中已收到良好的效果，它不仅较好地达到复习能量规律分析物理问题，还能较好地训练学生的思维方法，通过分析、归纳、演绎、渗透、想象、迁移等把握事物的内部联系，培养学生的各种能力。

作者介绍：程毓敏，江西省浮梁一中物理高级教师，

地　　 址： 江西省浮梁一中

邮　　 编： 333400

Email　： flyanzi@

电　　 话： 0798-8691718，15079848405

7．所有力做功的代数和(总功)等于物体动能的增量，即(动能定理)。

如果所研究的物体同时受几个力的作用，而这几个力中只有一个力是变力，其余均为恒力，且这些恒力所做的功和物体动能的变化量容易计算时，用动能定理求功是行之有效的。

　例9.质量为m的物体放在水平转台上，它与转台之间的摩擦因数为μ，物体与转轴相距R，物块随转台由静止开始转动。当转速增大到最大时，物体即将在转台上滑动，此时，转台己开始做匀速转动，在这一过程中，摩擦力对物体做的功为(　　 ) 　A.0　　 B.2πμmgR　　 C.2μmgR　　 D.μmgR/2 　解析：很明显，用直接求功法解此题很困难，但由于物体在转速最大时，它做圆周运动的向心力正好是它受到的最大静摩擦力，即有：μmg =mv²／R，可以求出它的最大速度，而整个过程只有静摩擦力对物体做功，故根据动能定理可以求出摩擦力对其做的功：W=mv²／2=μmgR／2。故选D。

例10. 质量为2kg的均匀链条自然堆放在光滑的水平面上，用20N竖直向上的拉力提起此链条，已知整个链条离地瞬间的速度v=7m/s，求拉力F所做功W之值。(取g=10m/s²)

解析： 作用在链条上的拉力虽然是恒力，但链条上提过程中提起部分的重力逐渐增大，故作用在整个链条上的合力为逐渐减小的变力，链条做变加速运动，难以应用牛顿定律求解。若用功能原理处理运动全过程，则可化难为易。设链长为L，则其重心向上位移H=L/2，根据动能定理， ，

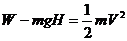即 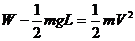　①

又由功的定义 W= FL 即L=W/F ②

将式②代入式①，解得：W= 98J。

小结：利用动能定理可以求变力做功，但不能用功的定义式直接求变力功，并且用动能定理只要求始末状态，不要求中间过程。这是动能定理比牛顿运动定律优越的一个方面。

6.2电磁感应现象中，感应电流在磁场中受到的安培力作了多少功就有多少电能产生，而这些电能又通过电流做功转变成其他能，如电阻上产生的焦耳热Q = W_A

例8.、如图6所示，倾角θ=30⁰，宽度L=1m的足够长的U形平行光滑金属导轨，导轨电阻不计，固定在磁感强度B=1T的范围充分大的匀强磁场中，磁场方向垂直导轨平面斜向上。用平行导轨功率恒为6W的牵引力F牵引一根质量为m=0.2Kg，电阻R=1Ω的金属棒ab由静止沿导轨向上移动，当ab移动S=2.8m时，获得稳定速度，在此过程中金属棒产生的焦耳热为5.8J(不计一切摩擦，g取10m/s²).问：金属棒从静止达到稳定速度所需的时间是多少？

解析：对导体棒受力分析如图7所示，可知导体棒达到稳定速度时：

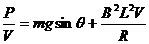
据功能关系，导体棒克服安培力做功:

W_A = Q =5.8J

又据动能定理：合外力做的总功等于动能的增量

Pt-mgh-W_A=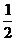mv²

解得V=2m/s ，　　　　　　　　　　　　　　　　　　　　　　　　　　　　

联立求解得：t=1.5s.

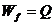6.1通电导线在磁场中受到安培力的作用而驱动，此时安培力做正功，能的转化是由电能转化为机械能。

6．磁场中的功和能是通过安培力做功来量度的。

5．一对滑动摩擦力所做功的代数和的绝对值等于摩擦所产生的内能，即。

4．除重力(和弹簧弹力)以外的力对物体所做的功，等于物体机械能的增量，　

3.电场力做功等于电势能的减少。

2.弹簧弹力做功等于弹性势能的减少。