26.(本小题满分16分)
解:(Ⅰ)函数的图象关于原点对称,
∴b=0, ………………(2分)
∴,
由,且解得
∴, ………………(6分)
(Ⅱ)过A、B的切线斜率分别是
若,则∴
由于(等号当且仅当两数至少一个为零时取得),
而(等号当且仅当两数一个为1另一个为-1时取得),
故不可能相等,
∴过A点的切线不能与过B点的切线垂直。………………(10分)
(Ⅲ)解法一:当时,切线斜率,∴,
过、的割线的斜率的绝对值恰为,
故。………………………………(16分)
解法二:
∵,∴,
又因为,
∴成立。………(16分)
点评:本题将导数知识与曲线的切线等几何因素以及不等式等相关知识有机地结合在一起,反映了高中数学的综合性和交汇性,考查了学生综合运用知识的能力。
20.(本小题满分14分)
解:(Ⅰ)
得
点的轨迹C的方程为………………(5分)
(Ⅱ)由得
由于直线与椭圆有两个交点, ①………………(8分)
(1)当,设P为弦MN的中点,
从而
又|AM|=|AN|,
则 即 ②
把②代入①得,解得;由②得,解得,
故所求m的取值范围是( ………………(11分)
(2)当时,|AM|=|AN|,
故所求m的取值范围是(-1,1). ………………(13分)
当时,m的取值范围是,当时,m的取值范围是(-1,1).…(14分)
点评:本题将向量知识与解析几何糅合到一起,体现了“数”与“形”的交汇,反映出了近年来高考数学考查的方向和热点。
解法一:
(Ⅰ)建立如图所示的空间直角坐标系.
设,
则,
于是.
………………(3分)
,
异面直线与所成的角为.………………(8分)
(Ⅱ),
. 则.…………(11分)
平面. 又平面,
平面平面. ………………(14分)
解法二:
(Ⅰ)连结交于点,取中点,连结,则∥.
设,
则 ,
.
.
中,,,
直三棱柱中,,则.
. ………………(6分)
,
异面直线与所成的角为.………………(8分)
(Ⅱ)直三棱柱中,,平面.
则. ………………(10分)
又,,,
则, 于是.
平面. 又平面,
平面平面. ………………(14分)
点评:两种思路,从两个不同角度研究了直三棱柱背景下线面位置关系与数量关系。

 的反函数是
的反函数是 的通项公式为
的通项公式为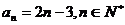 ,其前n项和为
,其前n项和为 ,则使
,则使 成立的n的最小值为
成立的n的最小值为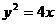 上点
上点 到焦点F的距离为
到焦点F的距离为 B.
B.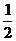 C.
C.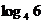 D.2
D.2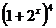 的展开式的第3项为12,则x等于
的展开式的第3项为12,则x等于 中,
中, ,如果
,如果 ,那么“
,那么“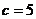 ”是“
”是“ 两个集合
两个集合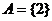 ,
, ,则
等于
,则
等于