3. 已知a,b,c满足c<b<a,且ac<0,则下列选项中不一定能成立的是 A.ab>ac B.c (b-a)>0 C.cb2<ca2 D.ac (a-c)<0
22. (本大题满分12分)定义在区间(0,+∞)上的函数f (x)满足对任意的实数x、y都有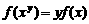 .
(1)求f (1)的值;
(2)若a>b>c>1,且a,b,c成等比数列,求证:
.
(1)求f (1)的值;
(2)若a>b>c>1,且a,b,c成等比数列,求证: ;
(3)若
;
(3)若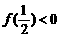 ,求证:f (x)在(0,+∞)上为增函数.
,求证:f (x)在(0,+∞)上为增函数.
21.
|
 轴于点P,交线段AB于点Q.
(1)试用t表示切线PQ的方程;
(2)设△QAP的面积为g (t),若函数g (t)在(m,n)上单调递减,试求出m的最小值;
(3)当
轴于点P,交线段AB于点Q.
(1)试用t表示切线PQ的方程;
(2)设△QAP的面积为g (t),若函数g (t)在(m,n)上单调递减,试求出m的最小值;
(3)当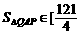 ,64]时,试求出点P横坐标的取值范围.
,64]时,试求出点P横坐标的取值范围.
20. (本大题满分12分)从4月1日开始,有一新款服装投入某商场销售,4月1日该款服装仅销售出20件,第二天销售出25件,第三天销售出40件,以后,每天售出的件数分别递增15件,直到日销售量达到最大,然后每天销售的件数分别递减10件.到月底该服装共销售出2 850件. (1)4月几号该款服装日销售量最大?其最大值是多少? (2)按规律,当该商场销售此服装超过1 300件时,社会上就流行,而日销售量连续下降,当日销售量低于100件时,则流行消失,问:该款服装在社会上流行是否超过10天?说明理由.
|

|
19. (本大题满分12分)数列{an}的前n项和为Sn,已知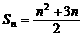 .
(1)求数列{an}的通项公式;
(2)若数列{cn}满足
.
(1)求数列{an}的通项公式;
(2)若数列{cn}满足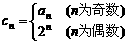 ,数列{cn}的前n项和为Tn,求Tn;
(3)张三同学利用第(2)题中的Tn设计了一个程序流程如图,但李四同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束).你是否同意李四同学的观点?请说明理由.
,数列{cn}的前n项和为Tn,求Tn;
(3)张三同学利用第(2)题中的Tn设计了一个程序流程如图,但李四同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束).你是否同意李四同学的观点?请说明理由.
18. (本大题满分12分)已知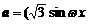 ,1),
,1),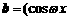 ,0),其中
,0),其中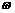 >0,又函数f (x)
>0,又函数f (x) 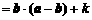 是以
是以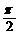 为最小正周期的周期函数,当x∈[0,
为最小正周期的周期函数,当x∈[0,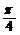 ]时,函数f (x)的最小值为-2.
(1)求f (x)的解析式;
(2)写出函数f (x)的单调递增区间;
(3)将函数f (x)的图象沿向量m平移后可以得到一个偶函数的图象,请写出一个符合条件的向量m.
]时,函数f (x)的最小值为-2.
(1)求f (x)的解析式;
(2)写出函数f (x)的单调递增区间;
(3)将函数f (x)的图象沿向量m平移后可以得到一个偶函数的图象,请写出一个符合条件的向量m.
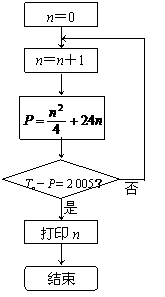

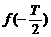 的值为
A.
的值为
A.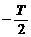 B.
B.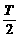 C.0 D.T
C.0 D.T ),则a的值为
A.
),则a的值为
A.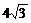 B.
B. C.
C.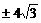 D.
D.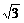
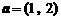 ,
,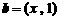 ,
,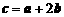 ,
,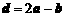 ,且
,且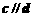 ,则实数x的值等于
A.
,则实数x的值等于
A.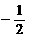 B.
B.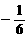 C.
C.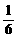 D.
D.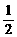
 ∁UB B.
∁UB B.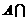 ∁UB
C.∁UB D.∁UA
∁UB
C.∁UB D.∁UA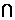 ∁UB
∁UB