23. (本题满分14分)
已知函数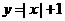 ,
,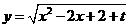 ,
,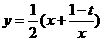
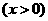 的最小值恰好是方程
的最小值恰好是方程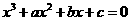 的三个根,其中
的三个根,其中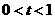 .
.
(Ⅰ)求证: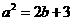 ;
;
(Ⅱ)设 ,
, 是函数
是函数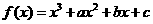 的两个极值点.
的两个极值点.
①若 ,求函数
,求函数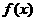 的解析式;
的解析式;
②求 的取值范围.
的取值范围.
22. (本题满分14分)
已知P是椭圆C: 上异于长轴端点的任意一点,A为长轴的左端点,F为椭圆的右焦点,椭圆的右准线与x轴、直线AP分别交于点K、M,
上异于长轴端点的任意一点,A为长轴的左端点,F为椭圆的右焦点,椭圆的右准线与x轴、直线AP分别交于点K、M,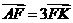 .
.
(Ⅰ)若椭圆的焦距为6,求椭圆C的方程;
(Ⅱ)若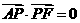 ,求证:
,求证: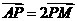 .
.

21. (本题满分14分)
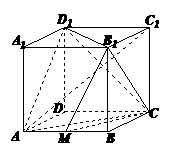
如图,正方体ABCD-A1B1C1D1的棱长为1, M是棱AB的中点.
(Ⅰ)求CD与平面AC D1所成的角;
(Ⅱ)求证:平面B1C D1⊥平面B1CM;
(Ⅲ)求点A1到平面B1CM 的距离.
20. (本题满分12分)
如图,摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
(Ⅰ)已知在时刻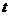 (min)时点P距离地面的高度
(min)时点P距离地面的高度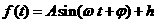 ,求2006min时点P距离地面的高度;
,求2006min时点P距离地面的高度;
(Ⅱ)求证:不论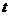 为何值,
为何值,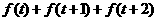 是定值.
是定值.

19. (本题满分12分)
数列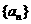 的前项
的前项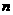 和记为
和记为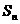 ,数列
,数列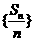 是首项为2,公比也为2的等比数列.
是首项为2,公比也为2的等比数列.
(Ⅰ)求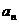 ;
;
(Ⅱ)若数列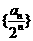 的前
的前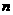 项和不小于100,问此数列最少有多少项?
项和不小于100,问此数列最少有多少项?
18. 假设要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,先将800袋牛奶按000,001,…,799进行编号,如果从随机数表第8行第18列的数开始向右读,请你依次写出最先检测的5袋牛奶的编号 ☆ .(下面摘取了一随机数表的第7行至第9行)
……
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 62 58 79
73 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
……

 ,
,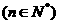 ,且
,且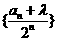 为等差数列,则
为等差数列,则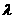 的值是 ☆ .
的值是 ☆ .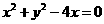 在点
在点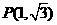 处的切线方程为
☆ .
处的切线方程为
☆ .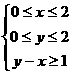 下,
下, 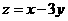 的最大值是 ☆ .
的最大值是 ☆ . 