17.(本小题满分12分)
已知函数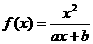 (a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(a,b为常数)且方程f(x)-x+12=0有两个实根为x1=3,
x2=4.
(1)求函数f(x)的解析式;
(2)设k>1,解关于x的不等式;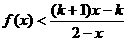 .
.
16.以下同个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,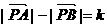 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若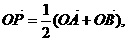 则动点P的轨迹为椭圆;
则动点P的轨迹为椭圆;
③方程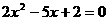 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
22、解:
(1)
将条件变为:1-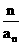 =
=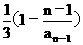 ,因此{1-
,因此{1-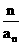 }为一个等比数列,其首项为
}为一个等比数列,其首项为
1- =
= ,公比
,公比 ,从而1-
,从而1-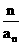 =
= ,据此得an=
,据此得an=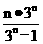 (n³1)…………1°
(n³1)…………1°
(2)
证:据1°得,a1·a2·…an=
为证a1·a2·……an<2·n!
只要证nÎN*时有 >
>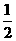 …………2°
…………2°
显然,左端每个因式都是正数,先证明,对每个nÎN*,有
 ³1-(
³1-( )…………3°
)…………3°
用数学归纳法证明3°式:
(i) n=1时,3°式显然成立,
(ii) 设n=k时,3°式成立,
即 ³1-(
³1-( )
)
则当n=k+1时,
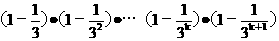 ³(1-(
³(1-( ))·(
))·( )
)
=1-( )-
)- +
+ (
( )
)
³1-( +
+ )即当n=k+1时,3°式也成立。
)即当n=k+1时,3°式也成立。
故对一切nÎN*,3°式都成立。
利用3°得, ³1-(
³1-( )=1-
)=1-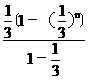
=1- >
>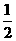
故2°式成立,从而结论成立。
b2(x1-x2)2x+a2(y1-y2)2y=0
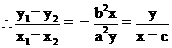
\b2x2+a2y2-b2cx=0…………(3)
2°当AB垂直于x轴时,点P即为点F,满足方程(3)
故所求点P的轨迹方程为:b2x2+a2y2-b2cx=0
(2)因为,椭圆 Q右准线l方程是x= ,原点距l
,原点距l
的距离为 ,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£
,由于c2=a2-b2,a2=1+cosq+sinq,b2=sinq(0<q£ )
)
则 =
= =2sin(
=2sin(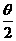 +
+ )
)
当q= 时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
时,上式达到最大值。此时a2=2,b2=1,c=1,D(2,0),|DF|=1
设椭圆Q: 上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
上的点 A(x1,y1)、B(x2,y2),三角形ABD的面积
S=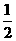 |y1|+
|y1|+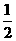 |y2|=
|y2|=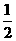 |y1-y2|
|y1-y2|
设直线m的方程为x=ky+1,代入 中,得(2+k2)y2+2ky-1=0
中,得(2+k2)y2+2ky-1=0
由韦达定理得y1+y2= ,y1y2=
,y1y2=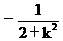 ,
,
4S2=(y1-y2)2=(y1+y2)2-4 y1y2=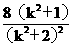
令t=k2+1³1,得4S2=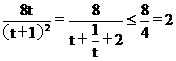 ,当t=1,k=0时取等号。
,当t=1,k=0时取等号。
因此,当直线m绕点F转到垂直x轴位置时,三角形ABD的面积最大。
22、(本大题满分14分)
已知数列{an}满足:a1= ,且an=
,且an=
(1) 求数列{an}的通项公式;
(2) 证明:对于一切正整数n,不等式a1·a2·……an<2·n!
21、解:如图,(1)设椭圆Q: (a>b>0)
(a>b>0)
上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则

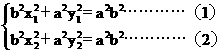
1°当AB不垂直x轴时,x1¹x2,
21、(本大题满分12分)
如图,椭圆Q: (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(1) 求点P的轨迹H的方程
(2) 在Q的方程中,令a2=1+cosq+sinq,b2=sinq(0<q£ ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
20、解法一:
(1)
方法一:作AH^面BCD于H,连DH。
AB^BDÞHB^BD,又AD= ,BD=1
,BD=1
\AB= =BC=AC \BD^DC
=BC=AC \BD^DC
又BD=CD,则BHCD是正方形,则DH^BC\AD^BC
方法二:取BC的中点O,连AO、DO
则有AO^BC,DO^BC,\BC^面AOD
\BC^AD
(2)
作BM^AC于M,作MN^AC交AD于N,则ÐBMN就是二面角B-AC-D的平面角,因为AB=AC=BC= \M是AC的中点,且MN¤¤CD,则BM=
\M是AC的中点,且MN¤¤CD,则BM=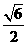 ,MN=
,MN=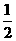 CD=
CD=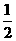 ,BN=
,BN=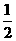 AD=
AD= ,由余弦定理可求得cosÐBMN=
,由余弦定理可求得cosÐBMN=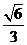
\ÐBMN=arccos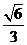
(3)
设E是所求的点,作EF^CH于F,连FD。则EF¤¤AH,\EF^面BCD,ÐEDF就是ED与面BCD所成的角,则ÐEDF=30°。设EF=x,易得AH=HC=1,则CF=x,FD=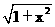 ,\tanÐEDF=
,\tanÐEDF= =
= =
= 解得x=
解得x= ,则CE=
,则CE= x=1
x=1
故线段AC上存在E点,且CE=1时,ED与面BCD成30°角。
解法二:此题也可用空间向量求解,解答略

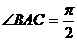 ,则PA与底面ABC所成角为
,则PA与底面ABC所成角为  设实数x,
y满足
设实数x,
y满足 .
. 是奇函数,则a=
.
是奇函数,则a=
.