(11)二项式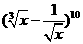 的展开式中常数项为
.
的展开式中常数项为
.
[思路点拨]本题考查二项式定理的通项公式,只要概念清楚和运算无误即可.
[正确解答]展开式的一般项为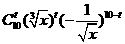 ,令
,令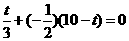 ,
, ,因此常数项为
,因此常数项为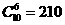 .
.
[解后反思]要注意符号因子不能丢.
(12)已知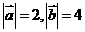 ,
,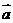 和
和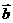 的夹角为
的夹角为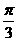 ,以
,以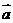 ,
,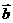 为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
.
为邻边作平行四边形,则此平行四边形的两条对角线中较短的一条的长度为
.
[思路点拨]本题以向量为背景,考查余弦定理,要判断较短的一条应是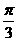 所对的对角线.
所对的对角线.
[正确解答]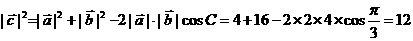
[解后反思]要正确向量的加减法则的几何意义,对向量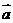 =(x,y)的模有几种方法.①
=(x,y)的模有几种方法.①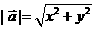 ②
②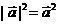 .
.
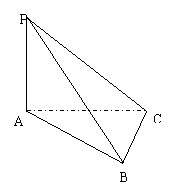 (13)如图,
(13)如图,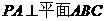 ,
,
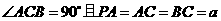 ,
,
则异面直线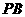 与
与 所成的角的正切值等于
.
所成的角的正切值等于
.
见理第12题
(14)在数列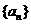 中,
中,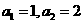 ,且
,且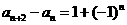
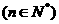 ,则
,则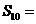 .
.
见理第13题
(15)设函数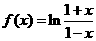 ,则函数
,则函数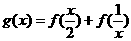 的定义域为
.
的定义域为
.
[思路点拨]本题考查复合函数定义域的求法,必须使常见各类函数都有意义,构成不等式组来解.
[正确解答]由题意得
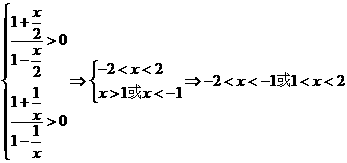 则所求定义域为
则所求定义域为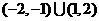 .
.
 [解后反思]正确地解不等式组,将繁分式化简是一关键.
[解后反思]正确地解不等式组,将繁分式化简是一关键.
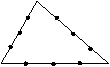
(16)在三角形的每条边上各取三个分点(如图).以
这9个分点为顶点可画出若干个三角形,若从中
任意抽取一个三角形,则其三个顶点分别落在原
三角形的三个不同边上的概率为 .
[思路点拨]本题考查等可能事件的概率,关键是要确定基本事件.
[正确解答]可画出的三角形个数为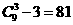 ,三个顶点分别落在不同边上的个数为
,三个顶点分别落在不同边上的个数为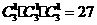 ,所求概率为
,所求概率为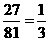 .
.
[解后反思]理解和掌握等可能事件的概率的计算公式P(A)=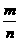 ,本题中构成三角形的个数是一难点.
,本题中构成三角形的个数是一难点.
- 答案

