(17)(本小题满分12分)
已知 ,求
,求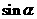 及
及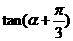 .
.
[思路点拨]本题以三角函数的求值问题考查三角变换能力和运算能力,可从已知角和所求角的内在联系(均含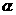 )进行转换得到.
)进行转换得到.
[正确解答]解法一:由题设条件,应用两角差的正弦公式得
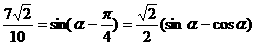 ,即
,即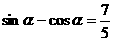 ①
①
由题设条件,应用二倍角余弦公式得
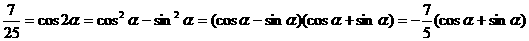
故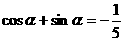 ②
②
由①和②式得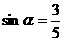 ,
,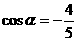

因此,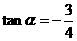 ,由两角和的正切公式
,由两角和的正切公式
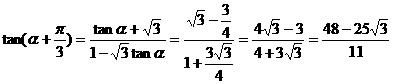
解法二:由题设条件,应用二倍角余弦公式得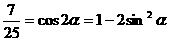 ,
,
解得 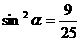 ,即
,即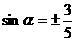

由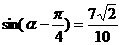 可得
可得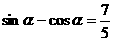

由于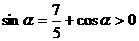 ,且
,且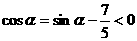 ,故a在第二象限
,故a在第二象限 于是
于是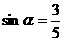 ,
,
从而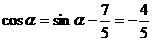

以下同解法一
[解后反思]在求三角函数值时,必须对各个公式间的变换应公式的条件要理解和掌握,注意隐含条件的使用,以防出现多解或漏解的情形.
(18)(本小题满分12分)
若公比为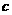 的等比数列
的等比数列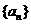 的首项
的首项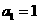 且满足
且满足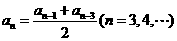 .
.
(I)求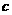 的值;
的值;
(II)求数列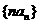 的前
的前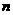 项和
项和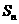 .
.
[思路点拨]本题考查等比数列的通项公式及前n项和的求法.可根据其定义进行求解,要注意①等比数列的公比C是不为零的常数②前n项和的公式是关于n的分段函数,对公比C是否为1加以讨论.
[正确解答](Ⅰ)解:由题设,当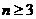 时,
时,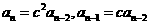 ,
,
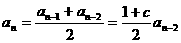 ,
,
由题设条件可得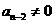 ,因此
,因此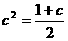 ,即
,即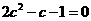

解得c=1或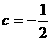

(Ⅱ)解:由(Ⅰ),需要分两种情况讨论,
当c=1时,数列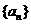 是一个常数列,即
是一个常数列,即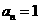 (nÎN*)
(nÎN*)
这时,数列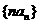 的前n项和
的前n项和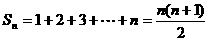

当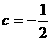 时,数列
时,数列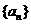 是一个公比为
是一个公比为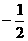 的等比数列,即
的等比数列,即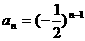 (nÎN*)
(nÎN*)
这时,数列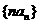 的前n项和
的前n项和
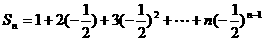 ①
①
① 式两边同乘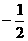 ,得
,得
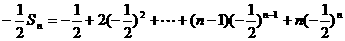 ②
②
①式减去②式,得
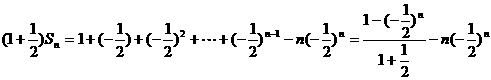
所以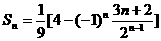 (nÎN*)
(nÎN*)
[解后反思]本题是数列求和及极限的综合题.
(1)完整理解等比数列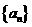 的前n项和公式:
的前n项和公式: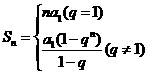
(2)要掌握以下几种情形的极限的求法.①利用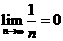 ②利用
②利用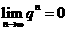 (
(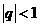 )③要掌握分类讨论的背景转化方法.如
)③要掌握分类讨论的背景转化方法.如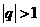 时转化为
时转化为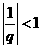 .
.
(19)(本小题满分12分)
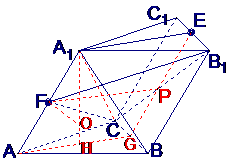 如图,在斜三棱柱
如图,在斜三棱柱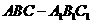 中,
中,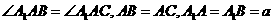 ,
,
侧面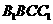 与底面
与底面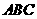 所成的二面角为
所成的二面角为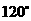 ,
,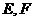 分别是棱
分别是棱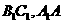 的中点
的中点
(I)求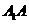 与底面
与底面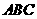 所成的角;
所成的角;
(II)证明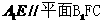 ;
;
(III)求经过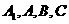 四点的球的体积.
四点的球的体积.
见理第19题
(20)(本小题满分12分)
某人在山坡 点处观看对面山顶上的一座铁塔,如图所示,塔高
点处观看对面山顶上的一座铁塔,如图所示,塔高 米,塔所在的山高
米,塔所在的山高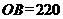 米,
米,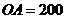 米,图中所示的山坡可视为直线
米,图中所示的山坡可视为直线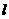 且点
且点 在直线
在直线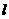 上,
上,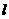 与水平面的夹角为
与水平面的夹角为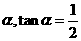 .试问,此人距水平地面多高时,观看塔的视角
.试问,此人距水平地面多高时,观看塔的视角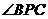 最大(不计此人身高)?
最大(不计此人身高)?
见理第20题
(21)(本小题满分14分)
已知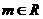 ,设
,设
 :
: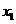 和
和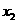 是方程
是方程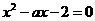 的两个实根,不等式
的两个实根,不等式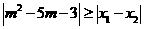 对任意实数
对任意实数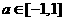 恒成立;
恒成立;
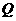 :函数
:函数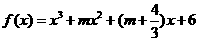 在
在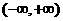 上有极值.
上有极值.
求使 正确且
正确且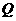 正确的
正确的 的取值范围.
的取值范围.
[思路点拨]本题是组合题,考查一元二次方程的根的概念和导数的应用.
[正确解答] (Ⅰ)由题设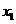 和
和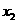 是方程
是方程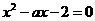 的两个实根,得
的两个实根,得
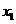 +
+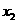 =
=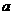 且
且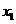
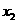 =-2,
=-2,
所以,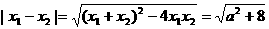
当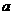 Î[-1,1]时,
Î[-1,1]时,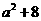 的最大值为9,即
的最大值为9,即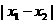 £3
£3
由题意,不等式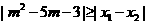 对任意实数
对任意实数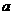 Î[1,1]恒成立的m的解集等于不等式
Î[1,1]恒成立的m的解集等于不等式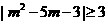 的解集
的解集 由此不等式得
由此不等式得
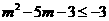 ①
①
或 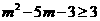 ②
②
不等式①的解为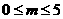

不等式②的解为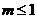 或
或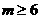

因为,对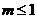 或
或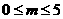 或
或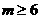 时,P是正确的
时,P是正确的
(Ⅱ)对函数 求导
求导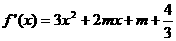
令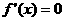 ,即
,即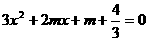
 此一元二次不等式的判别式
此一元二次不等式的判别式
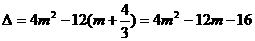

若D=0,则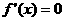 有两个相等的实根
有两个相等的实根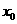 ,且
,且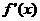 的符号如下:
的符号如下:
|
|
(-¥,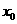 ) ) |
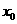 |
(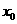 ,+¥) ,+¥) |
|
|
+ |
0 |
+ |
因为,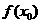 不是函数
不是函数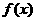 的极值
的极值
若D>0,则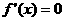 有两个不相等的实根
有两个不相等的实根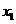 和
和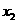 (
(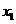 <
<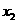 ),且
),且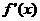 的符号如下:
的符号如下:
|
x |
(-¥,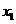 ) ) |
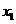 |
(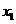 , ,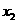 ) ) |
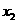 |
(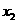 ,+¥) ,+¥) |
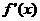 |
+ |
0 |
- |
0 |
+ |
因此,函数f(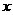 )在
)在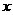 =
=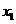 处取得极大值,在
处取得极大值,在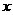 =
=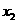 处取得极小值
处取得极小值
综上所述,当且仅当D>0时,函数f(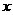 )在(-¥,+¥)上有极值
)在(-¥,+¥)上有极值
由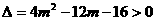 得
得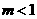 或
或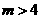 ,
,
因为,当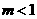 或
或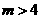 时,Q是正确得
时,Q是正确得
综上,使P正确且Q正确时,实数m的取值范围为(-¥,1)È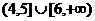

[解后反思]对恒成立问题的等价转换,相应知识的完整理解是关键.对P来说,转化为求使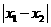 的最大值时的范围,而要注意一次二次方程根存在的充要条件.对Q来说,
的最大值时的范围,而要注意一次二次方程根存在的充要条件.对Q来说,
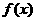 的导函数存在的充要条件的理解是一难点,也是易错点.
的导函数存在的充要条件的理解是一难点,也是易错点.
(22)(本小题满分14分)
抛物线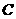 的方程为
的方程为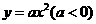 ,过抛物线
,过抛物线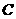 上的一点
上的一点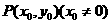 作斜率为
作斜率为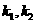 的两条直线分别交抛物线
的两条直线分别交抛物线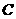 于
于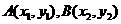 两点(
两点(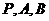 三点互不相同),且满足
三点互不相同),且满足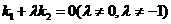 .
.
(I)求抛物线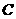 的焦点坐标和准线方程;
的焦点坐标和准线方程;
(II)设直线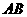 上一点
上一点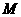 ,满足
,满足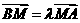 ,证明线段
,证明线段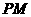 的中点在
的中点在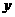 轴上;
轴上;
(III)当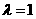 时,若点
时,若点 的坐标为(1,-1),求
的坐标为(1,-1),求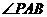 为钝角时点
为钝角时点 的纵坐标
的纵坐标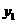 的取值范围.
的取值范围.
见理第22题.
- 答案

