(15)(本小题满分14分)
在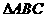 中,
中,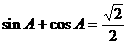 ,
,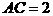 ,
,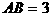 ,求
,求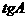 的值和
的值和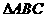 的面积
的面积
(16)(本小题满分14分)
如图,在正三棱柱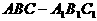 中,AB=2,
中,AB=2,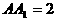 ,由顶点B沿棱柱侧面经过棱
,由顶点B沿棱柱侧面经过棱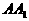 到顶点
到顶点 的最短路线与
的最短路线与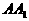 的交点记为M,求:
的交点记为M,求:
(I)三棱柱的侧面展开图的对角线长
(II)该最短路线的长及 的值
的值
(III)平面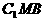 与平面ABC所成二面角(锐角)的大小
与平面ABC所成二面角(锐角)的大小

(17)(本小题满分14分)
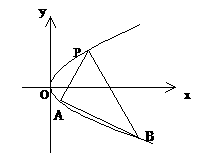
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2),A(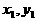 ),B(
),B(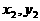 )均在抛物线上。
)均在抛物线上。
(I)写出该抛物线的方程及其准线方程
(II)当PA与PB的斜率存在且倾斜角互补时,求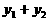 的值及直线AB的斜率
的值及直线AB的斜率
(18)(本小题满分14分)
函数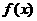 定义在[0,1]上,满足
定义在[0,1]上,满足 且
且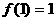 ,在每个区间
,在每个区间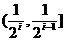 (
(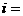 1,2……)上,
1,2……)上,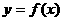 的图象都是平行于x轴的直线的一部分。
的图象都是平行于x轴的直线的一部分。
(I)求 及
及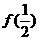 ,
,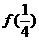 的值,并归纳出
的值,并归纳出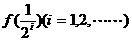 的表达式
的表达式
(II)设直线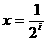 ,
,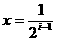 ,x轴及
,x轴及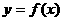 的图象围成的矩形的面积为
的图象围成的矩形的面积为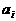 (
(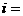 1,2……),求
1,2……),求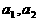 及
及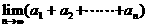 的值
的值
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=15km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度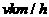 匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
匀速行驶,列车从A站到达某站的时间与时刻表上相应时间之差的绝对值称为列车在该站的运行误差。
(I)分别写出列车在B、C两站的运行误差
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求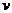 的取值范围
的取值范围
(20)(本小题满分12分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将这些数按下列要求进行分组,每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差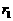 与所有可能的其他选择相比是最小的,
与所有可能的其他选择相比是最小的,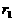 称为第一组余差;
称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为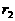 ;如此继续构成第三组(余差为
;如此继续构成第三组(余差为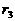 )、第四组(余差为
)、第四组(余差为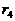 )、……,直至第N组(余差为
)、……,直至第N组(余差为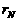 )把这些数全部分完为止。
)把这些数全部分完为止。
(I)判断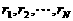 的大小关系,并指出除第N组外的每组至少含有几个数
的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n<N)组后,指出余下的每个数与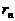 的大小关系,并证明
的大小关系,并证明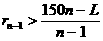
(III)对任何满足条件T的有限个正数,证明: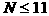
- 答案

