科目:,来源:,题型:
22. (本小题满分14分)
已知点G是ΔABC的重心,A(0,-1),B(0,1),在x轴上有一点M,满足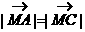 ,
,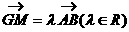
(1)求点C的轨迹方程;
(2)若斜率为k的直线l与点C的轨迹交于不同两点P,Q,且满足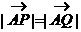 ,试求k的取值范围。
,试求k的取值范围。
点击展开完整题目
试题详情
科目:,来源:,题型:
21. (本小题满分12分)
已知数列{an}的首项a1=1,前n项的和Sn满足关系式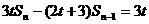 (
(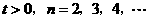 )
)
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比为f(t),作数列{bn},使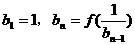 ,(n=2,3,4,……),求bn;
,(n=2,3,4,……),求bn;
(3)求 的和。
的和。
点击展开完整题目
试题详情
科目:,来源:,题型:
20. (本小题满分12分)
已知:命题p: 是
是 的原函数,且
的原函数,且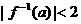 ;命题q:集合
;命题q:集合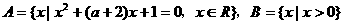 ,且
,且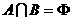
(1)求不等式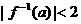 ;
;
(2)求使命题p、q中有且只有一个真命题时实数a的取值范围。
点击展开完整题目
试题详情
科目:,来源:,题型:
19. (本小题满分12分)
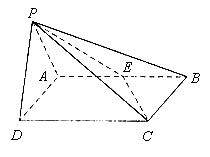
如图,在四棱锥P-ABCD中,侧面PAD是正三角形且与底面ABCD垂直,底面ABCD是矩形,E是AB中点,PC与平面ABCD所成角为30°。
(1)求二面角P-CE-D的大小;
(2)当AD为多长时,点D到平面PCE的距离为2。
点击展开完整题目
试题详情
科目:,来源:,题型:
18. (本小题满分12分)
现有甲、乙两只暗色口袋,已知甲口袋中装有白球2个,黑球2个,乙口袋内装有白球2个和黑球3个,且所有球只有颜色不同,其大小均相同。现从甲、乙两个口袋中各取1球交换后放回袋中。
(1)求甲口袋中恰有2个白球的概率;
(2)求甲口袋内白球数的数学期望。
点击展开完整题目
试题详情

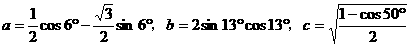 ,则有( )
,则有( )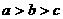 B.
B.
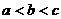 C.
C.
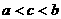 D.
D.
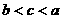
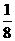 B.
B.
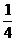 C.
C.
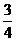 D.
D.
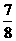
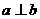 ”是“
”是“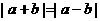 ”的( )
”的( )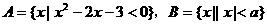 ,若
,若 ,则实数a的取值范围是( )
,则实数a的取值范围是( )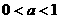 B.
B.
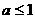 C.
C.
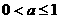 D.
D.


