22.(本小题满分14分)
(文科做)已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若a,b∈[-1,1],a+b≠0有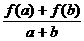 >0.
>0.
(1)判断函数f(x)在[-1,1]上是增函数,还是减函数,并证明你的结论;
(2)解不等式f(x+ )<f(
)<f(
(3)若f(x)≤m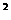 -2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
-2am+1,对所有x∈[-1,1],a∈[-1,1]恒成立,求实数m的取值范围.
(理科做)二次函数y=ax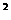 +x+1(a>0)的图象与x轴两个交点的横坐标分别为x
+x+1(a>0)的图象与x轴两个交点的横坐标分别为x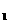 、x
、x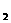 .
.
(1)证明(1+x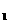 )·(1+x
)·(1+x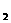 )=1;
)=1;
(2)证明x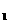 <-1,x
<-1,x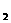 <-1;
<-1;
(3)若x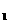 、x
、x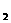 满足不等式|lg
满足不等式|lg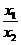 |≤1,试求a的取值范围.
|≤1,试求a的取值范围.
21.(本小题满分12分)
已知点P到两个定点A(1,0),B(2,0)的距离的比为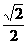 .
.
(1)求点P的轨迹C的方程;
(2)是否存在过点A(1,0)的直线l交轨迹C于M,N两点,使S =
=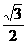 (O为坐标原点),若存在,求出l的方程;若不存在,说明理由.
(O为坐标原点),若存在,求出l的方程;若不存在,说明理由.
20.(本小题满分12分)
某商场预计全年分批购入每台价值为2000元的电视机共3600台,每批都购入x台(x∈N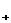 ),且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运费和保管费43600元.现在全年只有24000元资金可以用于支付这笔费用,请问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
),且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比.若每批购入400台,则全年需用去运费和保管费43600元.现在全年只有24000元资金可以用于支付这笔费用,请问能否恰当安排每批进货的数量,使资金够用?写出你的结论,并说明理由.
19.(本小题满分12分)
等比数列{a }同时满足下列三个条件:
}同时满足下列三个条件:
①a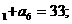 ②a
②a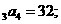 ③三个数4a
③三个数4a 依次成等差数列.
依次成等差数列.
(1)试求数列{a }的通项公式;
}的通项公式;
(2)记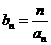 ,求数列{b
,求数列{b }的前n项和T
}的前n项和T ;
;
(2)(理科做)设S 是数列{a
是数列{a }的前n项和,证明
}的前n项和,证明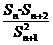 ≤1.
≤1.
18.(本小题满分12分)
已知A(3,0),B(0,3),C(cosα,sinα),O为坐标原点.
(1)若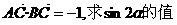 ;
;
(2)若| , 且α∈(0,π),求
, 且α∈(0,π),求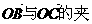 角.
角.
16.若干个能唯一确定一个数列的量称为该数列的“基本量”.设{a }是公比为q的无穷等
}是公比为q的无穷等
比数列,下列{a }的四组量中,一定能成为该数列“基本量”的是第_______组(写出所有符合要求的组号).①S
}的四组量中,一定能成为该数列“基本量”的是第_______组(写出所有符合要求的组号).①S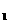 与S
与S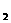 ; ②a
; ②a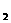 与S
与S ; ③a
; ③a 与a
与a ; ④q与a
; ④q与a .其中n为大于1的整数,S
.其中n为大于1的整数,S 为{a
为{a }的前n项和.
}的前n项和.

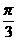 )的值.
)的值. x≥2,
x≥2,