22.(本题14分)(文)已知A、B、D三点不在一条直线上,且A(-2 ,0) ,
B(2 ,0),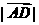 = 2 ,
= 2 ,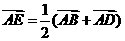
(1)求点E的轨迹方程;
(2)过点A作直线L交以A、B为焦点的椭圆于M、N两点。线段MN的中点到y轴距离为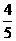 且直线MN与点E的轨迹相切,求椭圆的方程.
且直线MN与点E的轨迹相切,求椭圆的方程.
(理)在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足①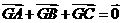 , ②
, ② =
=  =
= 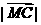 ③
③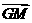 ∥
∥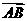
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为(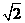 , 0) ,已知
, 0) ,已知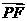 ∥
∥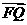 ,
, 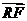 ∥
∥ 且
且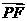 ·
·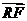 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
|
21.(本题12分)(文)已知函数f (x)
= a·bx的图像过点A(1, 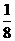 ), B (2 ,
), B (2 ,  )
)
(1 ) 求函数f ( x ) 的解析式.
(2)设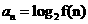 , n∈N+, Sn 是数列
, n∈N+, Sn 是数列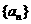 前n项和,求S20.
前n项和,求S20.
(3)在(2 )的条件下,若 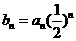 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(理)已知数列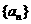 中各项为:
中各项为:
|
|
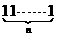
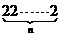 ……
……
(1)证明这个数列中的每一项都是两个相邻整数的积.
(2)求这个数列前n项之和Sn .
20.(本题12分)刘先生购买了一部手机,欲使用中国移动的“智慧”卡或加入中国联通网,经调查收费标准如下:
|
网络 |
月租 |
本地话费 |
长途话费 |
|
甲:联通 |
12元 |
0.3元/分钟 |
0.6元/分钟 |
|
乙:移动 |
无 |
0.5元/分钟 |
0.8元/分钟 |
|
(1)设刘先生每月通话时间为x分钟,求使用甲、乙两种入网方式所需话费的函数
f (x), g (x).
(2)请你根据刘先生每月通话时间为刘先生选择一种较为省钱的入网方式.
18.(本题12分)在四棱锥P-ABCD中,底面ABCD是边长为a的正方形, PA⊥平面ABCD,且PA = 2AB.
(1)求证:平面PAC⊥平面PBD
(2)求二面角B- PC - D的大小
17.(本题12分)已知f (x ) =
2cos2x +2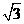 sinx cosx + a
(a为常数)
sinx cosx + a
(a为常数)
 (1)求f (x)的最小正周期 (2)求f (x)的单调递增区间
(1)求f (x)的最小正周期 (2)求f (x)的单调递增区间
(3)若f (x)在[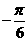 ,
, 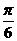 ]上最大值与最小值之和为3,求a的值.
]上最大值与最小值之和为3,求a的值.
16.设PQ是抛物线 y2 = 2px(p>0)上过焦点F的一条弦,L是抛物线的准线,给定下列命题:①以PF为直径的圆与y轴相切 , ②以QF为直径的圆与y轴相切, ③以PQ为直径的圆与准线L相切, ④以PF为直径的圆与y 轴相离 , ⑤以QF为直径的圆与y轴相交, 则其中所有正确命题的序号是:
15.设函数y = f (x)存在反函数且y = f ( x +3 )过点A (1 , 2 ) , 则y = f -1 (x+3)的 反函数必经过的点的坐标是

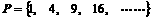 ,若
,若 ,
, ,则
,则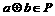 ,则运算
,则运算 可能是 ( )
可能是 ( ) 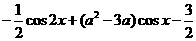 , 如果对 任意x∈R,不等式f (x ) + 4
≥0恒成立,求实数a的取值范围.
, 如果对 任意x∈R,不等式f (x ) + 4
≥0恒成立,求实数a的取值范围.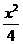 +
+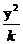 =1的离心率e = 2 ,则k的值为
=1的离心率e = 2 ,则k的值为
