20.若动圆C与圆(x-2)2+y2=1外切,且和直线x+1=0相切.求动圆圆心C的轨迹E的方程.
解:设动圆的圆心C的坐标为(x,y),则x-(-1)+1=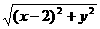 ,即x+2=
,即x+2=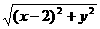 ,整理得y2=8x.所以所求轨迹E的方程为y2=8x.
,整理得y2=8x.所以所求轨迹E的方程为y2=8x.
21解:假设存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点.设l的方程为y=x+b,A(x1,y1),B(x2,y2).
由OA⊥OB知,kOA·kOB=-1,即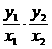 =-1,∴y1y2=-x1x2.
=-1,∴y1y2=-x1x2.
由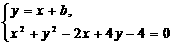 ,得2x2+2(b+1)x+b2+4b-4=0,
,得2x2+2(b+1)x+b2+4b-4=0,
∴x1+x2=-(b+1),x1·x2= +2b-2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2
+2b-2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2
=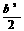 +2b-2-b(b+1)+b2=
+2b-2-b(b+1)+b2= +b-2
+b-2
∵y1y2=-x1x2 ∴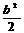 +b-2=-(
+b-2=-(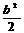 +2b-2) 即b2+3b-4=0.∴b=-4或b=1.
+2b-2) 即b2+3b-4=0.∴b=-4或b=1.
又Δ=4(b+1)2-8(b2+4b-4)=-4b2-24b+36=-4(b2+6b-9)
当b=-4时,Δ=-4×(16-24-9)>0; =1时,Δ=-4×(1+6-9)>0
故存在这样的直线l,它的方程是y=x-4或y=x+1,即x-y-4=0或x-y+1=0.
- 答案

