《2025年南通小题课时作业本四年级数学上册苏教版》

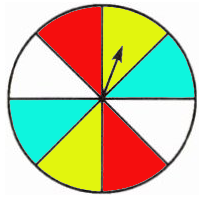
【反馈练习2】转动下面的转盘,若指针偶尔停在白色区域,则在下面的括号里画“√”。

(第三幅图)

答案： 第三幅图

【例3】设计一个转盘,转动指针,使指针停在红色区域和蓝色区域的可能性相等。

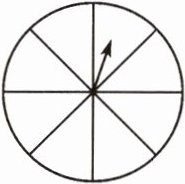
答案：
【分析】停在红色区域和蓝色区域的可能性相等,红色部分和蓝色部分的大小必须要相同。
【解答】
(1)把转盘涂满：

(2)只涂一部分：

【反馈练习3】在下面的转盘上涂色,转动指针,使指针停在红色、蓝色和黄色区域的可能性相等。

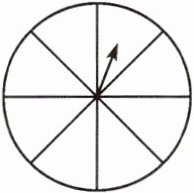
答案：

【例4】

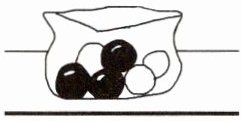
下面的说法对吗？对的画“√”,错的画“×”。
(1)每次任意摸一个球,再放回口袋,一共摸60次,白球和黑球一定会各摸到30次。(×)
(2)每次任意摸一个球,再放回口袋,一共摸60次,白球和黑球可能会各摸到30次。(√)

答案： 【分析】因为两种球个数相等,摸到的可能性相等,摸的次数越多,就接近。
【正确解答】
(1)×
(2)√
【错误解答】
(1)√
(2)×
【错因分析】只能说白球和黑球可能会各摸到30次,或白球和黑球摸到的次数差不多。