《2025年同步练习册分层卷八年级物理全一册沪科版》

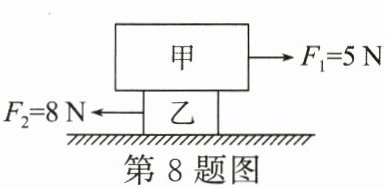
8. (3分)甲、乙两物体重叠并置于水平面上,当它们分别受到5N和8N的水平拉力时保持静止,如图所示。已知甲的底面积为$0.02m^{2}$,所受的重力为10N;乙的底面积为$0.01m^{2}$,所受的重力为20N。下列说法正确的是(B)

A.甲对乙的压强为500Pa
B.乙对地面的压力为30N
C.乙对甲的摩擦力大小为8N
D.地面对乙没有摩擦力的作用

答案： B 解析:甲对乙的压力F=Gₐ=10N,受力面积$ S_{乙}=0.01m^{2} $,甲对乙的压强$ p=\frac{F}{S_{乙}}=\frac{10N}{0.01m^{2}}=1000Pa $,故A错误;在水平面上,乙对地面的压力等于甲、乙所受的重力之和,即$ F_{乙}=G_{甲}+G_{乙}=10N+20N=30N $,故B正确;甲保持静止,所以乙对甲的摩擦力和甲受到的拉力是一对平衡力,大小相等,方向相反,则乙对甲的摩擦力为5N,故C错误;把甲、乙看作整体,整体受到F₁和F₂的合力$ F_{合}=F_{2}-F_{1}=8N-5N=3N $,由整体静止可知,地面对乙摩擦力的方向为水平向右,大小为$ f_{2}=F_{合}=3N $,故D错误。故选B。

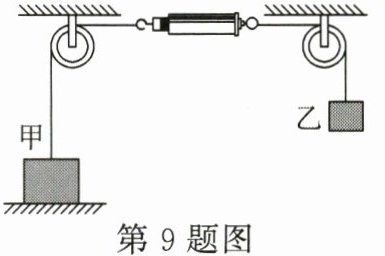
9. (4分)如图所示,甲物体重40N,乙物体重30N,甲、乙均静止,不计弹簧测力计自重及绳子与定滑轮之间的摩擦力,则弹簧测力计的示数为30N。如果甲物体是边长为10cm的正方体,则甲物体对水平地面的压强为1000Pa。

答案： 30 1000 解析:乙物体由于自身的重力对弹簧测力计施加了一个向右的30N的拉力,弹簧测力计的示数等于30N;甲物体受到竖直向上的拉力、竖直向上的支持力和竖直向下的重力,$ F_{支}=G_{甲}-F_{拉}=40N-30N=10N $。甲物体对水平地面的压力F=F支=10N,甲物体底面积S=10cm×10cm=100cm²=0.01m²,甲物体对水平地面的压强$ p=\frac{F}{S}=\frac{10N}{0.01m^{2}}=1000Pa $。

10. (6分)(2025·邵阳检测)如图所示,有两个正方体实心物体A、B叠放在水平桌面上,物体A重15N,B重5N。若物体B对A的压强与此时物体A对桌面的压强相等,则物体A对桌面的压力为$20$N,物体B对A的压力与物体A对桌面的压力之比是$1:4$,物体B与A的密度之比是$8:3$。

答案： 20 1:4 8:3 解析:物体A重15N,B重5N,所以物体B对A的压力为5N,物体A对桌面的压力为$ F_{A}=5N+15N=20N $;物体B对A的压力与物体A对桌面的压力之比是$ \frac{F_{B}}{F_{A}}=\frac{5N}{20N}=\frac{1}{4} $;因为物体A重15N,B重5N,物体B对A的压强$ p_{B}=\frac{G_{B}}{S_{B}}=\frac{5N}{L_{B}^{2}} $,物体A对桌面的压强$ p_{A}=\frac{G_{A}+G_{B}}{S_{A}}=\frac{15N+5N}{L_{A}^{2}} $,由题意可知$ p_{B}=p_{A} $,解得$ L_{A}=2L_{B} $。$ p_{B}=\frac{\rho _{B}V_{B}g}{S_{B}}=\frac{\rho _{A}V_{A}g+\rho _{B}V_{B}g}{S_{A}} $,整理可得$ \rho _{B}L_{B}=\rho _{A}L_{A}+\frac{\rho _{B}L_{B}^{3}}{L_{A}^{2}} $,解得$ \frac{\rho _{B}}{\rho _{A}}=\frac{8}{3} $。

11. (14分)(2025·北京检测)如图甲所示,底面积为$50cm^{2}$、高为10cm的平底圆柱形容器和一个质量为1kg、密度为$2.5g/cm^{3}$的小球置于水平桌面上(容器厚度不计)。容器内盛某种液体时,容器和液体的总质量与液体的体积关系如图乙所示。求:
(1)容器质量$m$;
(2)液体密度$ \rho_{液}$;
(3)若容器和液体的总质量为300g,将小球投入到容器的液体内,溢出液体的体积$V$;
(4)在第(3)问中,容器对桌面的压强$p$。

答案： 解:
(1)由题图乙可知,当V=0时,容器的质量$ m_{容器}=100g $。
（2）容器内盛某种液体,其体积$ V_{液}=200cm^{3} $时,容器和液体的总质量$ m_{总}=300g $,液体的质量$ m_{液}=m_{总}-m_{容器}=300g-100g=200g $,液体的密度$ \rho =\frac{m_{液}}{V_{液}}=\frac{200g}{200cm^{3}}=1g/cm^{3}=1× 10^{3}kg/m^{3} $。
(3)容器的体积$ V_{容}=Sh=50cm^{2}× 10cm=500cm^{3} $,容器和液体的总质量为300g时,容器内液体的体积$ V_{液}=200cm^{3} $,根据密度公式得,小球的体积$ V_{球}=\frac{m_{球}}{\rho _{球}}=\frac{1000g}{2.5g/cm^{3}}=400cm^{3} $,将小球投入到容器的液体内,溢出液体的体积$ V_{溢}=V_{液}+V_{球}-V_{容}=200cm^{3}+400cm^{3}-500cm^{3}=100cm^{3} $。
(4)根据密度公式得,溢出液体的质量$ m_{溢}=\rho V_{溢}=1g/cm^{3}× 100cm^{3}=100g $,容器对桌面的压强$ p=\frac{G_{总}+G_{球}-G_{溢}}{S}=\frac{(m_{总}+m_{球}-m_{溢})g}{S}=\frac{(300+1000-100)× 10^{-3}kg× 10N/kg}{50× 10^{-4}m^{2}}=2.4× 10^{3}Pa $。