2025年魔力暑假A计划八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年魔力暑假A计划八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 校园内有两棵树(如图),相距 8 m,一棵树高 13 m,另一棵树高 7 m. 一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞(

A.10 m
B.11 m
C.12 m
D.13 m
A
)
A.10 m
B.11 m
C.12 m
D.13 m
答案:
A
2. 如图,一轮船以每小时 18 n mile 的速度从港口 A 出发向西北方向航行,另一轮船以每小时 24 n mile 的速度同时从港口 A 出发向东北方向航行. 离开港口 1.5 h 后,两轮船相距(

A.30 n mile
B.35 n mile
C.40 n mile
D.45 n mile
D
)
A.30 n mile
B.35 n mile
C.40 n mile
D.45 n mile
答案:
D
3. 小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边 1.5 m 远的水底,竹竿高出水面 0.5 m. 把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为(
A.2 m
B.2.5 m
C.2.25 m
D.3 m
A
)A.2 m
B.2.5 m
C.2.25 m
D.3 m
答案:
A
4. (广西中考)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃一尺,不合二寸. 问门广几何. 题目大意是如图①,②(图②为图①的平面示意图),推开双门,双门间隙 CD 的距离为 2 寸,点 C 和点 D 距离门槛 AB 都为 1 尺(1 尺= 10 寸),则 AB 的长为( )

A.50.5 寸
B.52 寸
C.101 寸
D.104 寸

A.50.5 寸
B.52 寸
C.101 寸
D.104 寸
答案:
C 【解析】如图,取 AB 的中点 O,过点 D 作 DE⊥AB 于点 E.
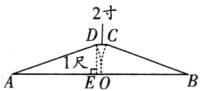
由题意,得 OA = OB = AD = BC.
设 OA = OB = AD = BC = r 寸,
则 AB = 2r 寸.
∵ DE = 10 寸,OE = $\frac{1}{2}$CD = 1 寸,
∴ AE = (r - 1) 寸.
在 Rt△ADE 中,AE² + DE² = AD²,即 (r - 1)² + 10² = r²,解得 r = 50.5,
∴ 2r = 101,
∴ AB = 101 寸.
C 【解析】如图,取 AB 的中点 O,过点 D 作 DE⊥AB 于点 E.

由题意,得 OA = OB = AD = BC.
设 OA = OB = AD = BC = r 寸,
则 AB = 2r 寸.
∵ DE = 10 寸,OE = $\frac{1}{2}$CD = 1 寸,
∴ AE = (r - 1) 寸.
在 Rt△ADE 中,AE² + DE² = AD²,即 (r - 1)² + 10² = r²,解得 r = 50.5,
∴ 2r = 101,
∴ AB = 101 寸.
5. 如图,有一块长为 24 m 的长方形土地,在土地旁边 B 处有健身器材. 居住在 A 处的居民最少走______步可到 B 处健身(假设 2 步为 1 m).

5. 如图,有一块长为 24 m 的长方形土地,在土地旁边 B 处有健身器材. 居住在 A 处的居民最少走____


5. 如图,有一块长为 24 m 的长方形土地,在土地旁边 B 处有健身器材. 居住在 A 处的居民最少走____
52
__步可到 B 处健身(假设 2 步为 1 m).
答案:
52
6. 如图,将一根长为 20 cm 的吸管,置于底面直径为 5 cm、高为 12 cm 的圆柱形水杯中. 设吸管露在杯子外面的长度为 h cm,则 h 的取值范围是______.


答案:
7 ≤ h ≤ 8 【解析】如图,当吸管、底面直径、杯子的高恰好构成直角三角形时,h 最小,
此时 AB = $\sqrt{5² + 12²}$ = 13,故 h_{最小} = 20 - 13 = 7;当吸管竖直插入水杯时,h 最大,此时 h_{最大} = 20 - 12 = 8. 故 h 的取值范围是 7 ≤ h ≤ 8.
7 ≤ h ≤ 8 【解析】如图,当吸管、底面直径、杯子的高恰好构成直角三角形时,h 最小,

此时 AB = $\sqrt{5² + 12²}$ = 13,故 h_{最小} = 20 - 13 = 7;当吸管竖直插入水杯时,h 最大,此时 h_{最大} = 20 - 12 = 8. 故 h 的取值范围是 7 ≤ h ≤ 8.
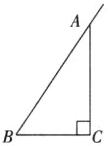
7. (永州道县期末)如下图,一根直立的旗杆高 8 m,因刮大风旗杆从点 C 处折断,顶部 B 着地且离旗杆底部 A 的距离为 4 m.
(1)求 AC 的高度;
(2)工人在修复的过程中,发现在折断点 C 的下方 1 m 的点 D 处,有一条明显裂痕. 将旗杆修复后,若下次大风将旗杆从点 D 处吹断,则距离旗杆底部周围多大范围内有被砸伤的风险?

(1)求 AC 的高度;
(2)工人在修复的过程中,发现在折断点 C 的下方 1 m 的点 D 处,有一条明显裂痕. 将旗杆修复后,若下次大风将旗杆从点 D 处吹断,则距离旗杆底部周围多大范围内有被砸伤的风险?

答案:
解:
(1) 由题意,得 AC + BC = 8 m.
设 AC 长为 x m,则 BC 长为 (8 - x) m.
∵ ∠A = 90°,
∴ 4² + x² = (8 - x)²,
解得 x = 3.
故旗杆距地面 3 m 处折断.
(2) 如图,设从点 D 处折断时,顶部 B 落在点 B' 处,连接 B'D.
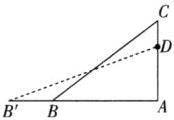
依题意,得 AD = 3 - 1 = 2(m),
∴ B'D = 8 - 2 = 6(m),
∴ AB' = $\sqrt{B'D² - AD²}$ = $\sqrt{6² - 2²}$ = $4\sqrt{2}$(m),
∴ 距离旗杆底部周围 $4\sqrt{2}$ m 的范围内有被砸伤的风险.
解:
(1) 由题意,得 AC + BC = 8 m.
设 AC 长为 x m,则 BC 长为 (8 - x) m.
∵ ∠A = 90°,
∴ 4² + x² = (8 - x)²,
解得 x = 3.
故旗杆距地面 3 m 处折断.
(2) 如图,设从点 D 处折断时,顶部 B 落在点 B' 处,连接 B'D.

依题意,得 AD = 3 - 1 = 2(m),
∴ B'D = 8 - 2 = 6(m),
∴ AB' = $\sqrt{B'D² - AD²}$ = $\sqrt{6² - 2²}$ = $4\sqrt{2}$(m),
∴ 距离旗杆底部周围 $4\sqrt{2}$ m 的范围内有被砸伤的风险.
查看更多完整答案,请扫码查看


