2025年魔力暑假A计划八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年魔力暑假A计划八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle A = 60^{\circ}$,$CD是斜边AB$上的高。若$AD = 3cm$,则斜边$AB$的长是(
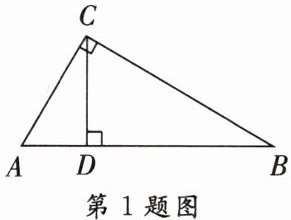
A.$3cm$
B.$6cm$
C.$9cm$
D.$12cm$
D
)
A.$3cm$
B.$6cm$
C.$9cm$
D.$12cm$
答案:
D
2. 如图所示的是某商场一楼与二楼之间的自动扶梯示意图,其中$AB$,$CD$分别表示一楼、二楼地面的水平线。若$\angle ABC = 150^{\circ}$,$BC$的长是$15m$,则乘自动扶梯从点$B$到点$C$上升的高度$h$是(

A.$\frac{15}{2}m$
B.$\frac{5}{2}\sqrt{3}m$
C.$5\sqrt{3}m$
D.$\frac{15}{2}\sqrt{3}m$
A
)
A.$\frac{15}{2}m$
B.$\frac{5}{2}\sqrt{3}m$
C.$5\sqrt{3}m$
D.$\frac{15}{2}\sqrt{3}m$
答案:
A
3. 如图,在矩形$ABCD$中,$AB = 3$,$BC = 4$,$E是边AD$上一点,$F$是矩形内一点,且$\angle BCF = 30^{\circ}$,则$EF + \frac{1}{2}CF$的最小值是( )
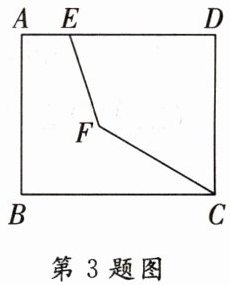
A.$3$
B.$4$
C.$5$
D.$2\sqrt{3}$

A.$3$
B.$4$
C.$5$
D.$2\sqrt{3}$
答案:
A [解析]如图,过点F作GH//CD,交AD于点G,BC于点H.
∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,AD//BC,
∴GH⊥AD,∠CHF=90°.
∵∠BCF=30°,
∴FH=$\frac{1}{2}$CF.
∵E是边AD上一点,
∴EF+$\frac{1}{2}$CF=EF+FH,
∴EF+$\frac{1}{2}$CF的最小值是GH.
∵∠GHC=∠BCD=∠D=90°,
∴四边形DGHC是矩形,
∴GH=CD=AB=3,
即EF+$\frac{1}{2}$CF的最小值是3.

A [解析]如图,过点F作GH//CD,交AD于点G,BC于点H.
∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,AD//BC,
∴GH⊥AD,∠CHF=90°.
∵∠BCF=30°,
∴FH=$\frac{1}{2}$CF.
∵E是边AD上一点,
∴EF+$\frac{1}{2}$CF=EF+FH,
∴EF+$\frac{1}{2}$CF的最小值是GH.
∵∠GHC=∠BCD=∠D=90°,
∴四边形DGHC是矩形,
∴GH=CD=AB=3,
即EF+$\frac{1}{2}$CF的最小值是3.

4. 如图,$\angle A = 30^{\circ}$,点$B$在射线$AM$上,且$AB = 2$,则点$B$到射线$AN$的距离是______。
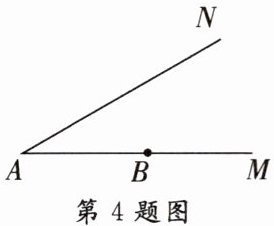
4. 如图,$\angle A = 30^{\circ}$,点$B$在射线$AM$上,且$AB = 2$,则点$B$到射线$AN$的距离是


4. 如图,$\angle A = 30^{\circ}$,点$B$在射线$AM$上,且$AB = 2$,则点$B$到射线$AN$的距离是
1
。
答案:
1
5. 如图,在$\triangle ABC$中,$\angle A = 90^{\circ}$,$\angle C = 75^{\circ}$,$AC = 6$,$DE$垂直平分$BC$,则$BE$的长为______

12
。
答案:
12
6. 如图①所示的是某超市入口的双翼闸门,它的平面示意图如图②所示。当它的双翼展开时,双翼边缘的端点$A与B之间的距离为10cm$,双翼的边缘$AC = BD = 54cm$,且与闸机侧立面的夹角$\angle PCA = \angle BDQ = 30^{\circ}$。当双翼收起时,可以通过闸机的物体的最大宽度为______$cm$。
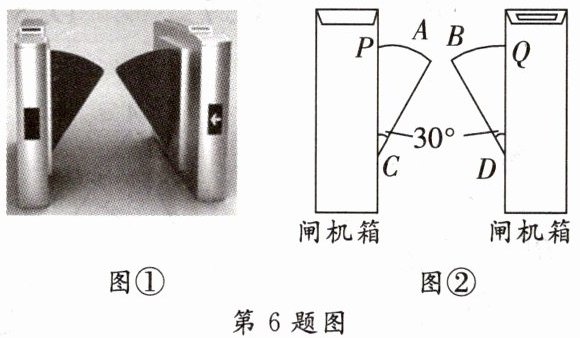

答案:
64 [解析]如图所示,过点A作AE⊥CP于点E,过点B作BF⊥DQ于点F.
∵∠PCA=30°,
∴在Rt△ACE中,AE=$\frac{1}{2}$AC=$\frac{1}{2}$×54=27(cm). 同理可得,BF=27cm. 又
∵点A与点B之间的距离为10cm,
∴可以通过闸机的物体的最大宽度为27+10 +27=64(cm).

64 [解析]如图所示,过点A作AE⊥CP于点E,过点B作BF⊥DQ于点F.
∵∠PCA=30°,
∴在Rt△ACE中,AE=$\frac{1}{2}$AC=$\frac{1}{2}$×54=27(cm). 同理可得,BF=27cm. 又
∵点A与点B之间的距离为10cm,
∴可以通过闸机的物体的最大宽度为27+10 +27=64(cm).

7. 如下图,一艘轮船自西向东航行,在$A处测得小岛P在北偏东75^{\circ}$方向上,航行$7n mile后到达B$处,在$B处测得小岛P在北偏东60^{\circ}$方向上。若小岛$P周围3.8n mile$内有暗礁,则该轮船继续向东航行,是否有触礁的危险?请说明理由。


答案:
解:有触礁的危险.
理由:如图,过点P作PD⊥直线AB于点D.
易知AB=7nmile,∠PAB=15°,∠PBD=30°,
∴∠APB=∠PBD−∠PAB=15°,
∴∠APB=∠PAB,
∴PB=AB=7nmile.
∵∠PDB=90°,∠PBD=30°,
∴PD=$\frac{1}{2}$PB=3.5nmile.
∵3.5<3.8,
∴该轮船继续向东航行,有触礁的危险.

解:有触礁的危险.
理由:如图,过点P作PD⊥直线AB于点D.
易知AB=7nmile,∠PAB=15°,∠PBD=30°,
∴∠APB=∠PBD−∠PAB=15°,
∴∠APB=∠PAB,
∴PB=AB=7nmile.
∵∠PDB=90°,∠PBD=30°,
∴PD=$\frac{1}{2}$PB=3.5nmile.
∵3.5<3.8,
∴该轮船继续向东航行,有触礁的危险.

查看更多完整答案,请扫码查看


