2025年魔力暑假A计划八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年魔力暑假A计划八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在$\triangle OAB$中,$∠O = 90^{\circ}$,$∠A = 35^{\circ}$,则$∠B = $(
A.$35^{\circ}$
B.$55^{\circ}$
C.$65^{\circ}$
D.$145^{\circ}$
B
)A.$35^{\circ}$
B.$55^{\circ}$
C.$65^{\circ}$
D.$145^{\circ}$
答案:
B
2. 如图,已知$l// AB$,$CD⊥l于点D$。若$∠C = 40^{\circ}$,则$∠1$的度数是(

A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
C
)
A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$60^{\circ}$
答案:
C
3. 具备下列条件的$\triangle ABC$,不是直角三角形的是(
A. $∠A + ∠B = ∠C$
B. $∠A - ∠B = ∠C$
C. $∠A:∠B:∠C = 1:2:3$
D. $∠A = ∠B = 3∠C$
D
)A. $∠A + ∠B = ∠C$
B. $∠A - ∠B = ∠C$
C. $∠A:∠B:∠C = 1:2:3$
D. $∠A = ∠B = 3∠C$
答案:
D
4. 如图,某同学在课桌上无意中将一块三角板叠放在直尺上,则$∠1 + ∠2$等于(
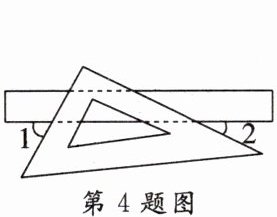
A.$60^{\circ}$
B.$75^{\circ}$
C.$90^{\circ}$
D.$105^{\circ}$
C
)
A.$60^{\circ}$
B.$75^{\circ}$
C.$90^{\circ}$
D.$105^{\circ}$
答案:
C
5. 如图,$CD是\triangle ABC$的中线,$∠ACB = 90^{\circ}$,$∠CDB = 100^{\circ}$,则$∠A$等于(

A.$20^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$
C
)
A.$20^{\circ}$
B.$45^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$
答案:
C 【解析】
∵CD是△ABC的中线,∠ACB=90°,
∴CD=$\frac{1}{2}$AB=BD,
∴∠B=∠BCD.
∵∠CDB=100°,
∴∠B=∠BCD=$\frac{1}{2}$(180°−∠CDB)=40°,
∴∠A=180°−∠ACB−∠B=50°.
∵CD是△ABC的中线,∠ACB=90°,
∴CD=$\frac{1}{2}$AB=BD,
∴∠B=∠BCD.
∵∠CDB=100°,
∴∠B=∠BCD=$\frac{1}{2}$(180°−∠CDB)=40°,
∴∠A=180°−∠ACB−∠B=50°.
6. 在$Rt\triangle ABC$中,$∠C = 90^{\circ}$,$∠A = ∠B$,那么$∠A$的度数为
45°
。
答案:
45°
7. 如图,一根木棍$AB$斜靠在与地面垂直的墙上,$P$为$AB$的中点。若木棍的$A$端沿墙下滑,$B$端沿地面向右滑行,在滑动的过程中,点$P$到点$C$的距离__
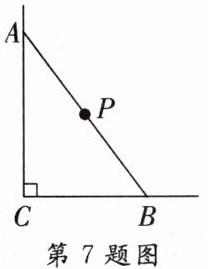
不会
__ (填“会”或“不会”)发生变化。理由是__直角三角形斜边上的中线$CP$等于斜边$AB$的一半
__。
答案:
不会 直角三角形斜边上的中线CP等于斜边AB的一半
8.(益阳南县期末)如图,在$Rt\triangle BAC和Rt\triangle BDC$中,$∠BAC = ∠BDC = 90^{\circ}$,$O是BC$的中点,连接$AO$,$DO$。若$AO = 3$,则$DO$的长为______

3
。
答案:
3
9. 如图,$∠O = 50^{\circ}$,$P是边OB$上一个动点(不与点$O$重合)。当$∠A$的度数为______时,$\triangle AOP$为直角三角形。

9. 如图,$∠O = 50^{\circ}$,$P是边OB$上一个动点(不与点$O$重合)。当$∠A$的度数为


9. 如图,$∠O = 50^{\circ}$,$P是边OB$上一个动点(不与点$O$重合)。当$∠A$的度数为
90°或40°
时,$\triangle AOP$为直角三角形。
答案:
90°或40° 【解析】根据题意可分以下两种情况:
①当∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
综上所述,当∠A的度数为90°或40°时,△AOP为直角三角形.
①当∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
综上所述,当∠A的度数为90°或40°时,△AOP为直角三角形.
10. 如下图,在$Rt\triangle ABC$中,$AB = AC$,$∠BAC = 90^{\circ}$,$O为BC$的中点。
(1)写出点$O$到$\triangle ABC$的三个顶点$A$,$B$,$C$的距离的数量关系,并说明理由;
解:(1)
(2)如果点$M$,$N$分别在线段$AB$,$AC$上移动,移动中保持$AN = BM$,判断$\triangle MON$的形状,并证明你的结论。
(2)

(1)写出点$O$到$\triangle ABC$的三个顶点$A$,$B$,$C$的距离的数量关系,并说明理由;
解:(1)
OA = OB = OC.理由如下:∵在$Rt\triangle ABC$中,$∠BAC = 90^{\circ}$,$O$为$BC$的中点,∴$OA = \frac{1}{2}BC = OB = OC$,即$OA = OB = OC.$
(2)如果点$M$,$N$分别在线段$AB$,$AC$上移动,移动中保持$AN = BM$,判断$\triangle MON$的形状,并证明你的结论。
(2)
$\triangle MON$是等腰直角三角形.证明如下:∵$AC = AB$,$OC = OB$,$∠BAC = 90^{\circ}$,∴$∠C = ∠B = 45^{\circ}$,$AO⊥BC.$∵$AO = OC$,∴$∠NAO = ∠C = ∠B.$又∵$AN = BM$,$OA = OB$,∴$\triangle AON≌\triangle BOM(SAS)$,∴$ON = OM$,$∠NOA = ∠MOB$,∴$∠NOA + ∠AOM = ∠MOB + ∠AOM$,∴$∠NOM = ∠AOB = 90^{\circ}$,∴$\triangle MON$是等腰直角三角形.

答案:
解:
(1)OA=OB=OC.理由如下:
∵在Rt△ABC中,∠BAC=90°,O为BC的中点,
∴OA=$\frac{1}{2}$BC=OB=OC,即OA=OB=OC.
(2)△MON是等腰直角三角形.证明如下:
∵AC=AB,OC=OB,∠BAC=90°,
∴∠C=∠B=45°,AO⊥BC.
∵AO=OC,
∴∠NAO=∠C=∠B.
又
∵AN=BM,OA=OB,
∴△AON≌△BOM(SAS),
∴ON=OM,∠NOA=∠MOB,
∴∠NOA+∠AOM=∠MOB+∠AOM,
∴∠NOM=∠AOB=90°,
∴△MON是等腰直角三角形.
(1)OA=OB=OC.理由如下:
∵在Rt△ABC中,∠BAC=90°,O为BC的中点,
∴OA=$\frac{1}{2}$BC=OB=OC,即OA=OB=OC.
(2)△MON是等腰直角三角形.证明如下:
∵AC=AB,OC=OB,∠BAC=90°,
∴∠C=∠B=45°,AO⊥BC.
∵AO=OC,
∴∠NAO=∠C=∠B.
又
∵AN=BM,OA=OB,
∴△AON≌△BOM(SAS),
∴ON=OM,∠NOA=∠MOB,
∴∠NOA+∠AOM=∠MOB+∠AOM,
∴∠NOM=∠AOB=90°,
∴△MON是等腰直角三角形.
查看更多完整答案,请扫码查看


