2025年魔力暑假A计划八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年魔力暑假A计划八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如右图,在$□ ABCD$中,$AB = 2$,$AD = 1$,$\angle ADC = 60^{\circ}$.将$□ ABCD$沿过点A的直线l折叠,使点D落在AB边上的点$D'$处,折痕交CD边于点E.
(1)求证:四边形$BCED'$是菱形;
(2)若P是直线l上的一个动点,请计算$PD' + PB$的最小值.

(1)求证:四边形$BCED'$是菱形;
(2)若P是直线l上的一个动点,请计算$PD' + PB$的最小值.

答案:
解:
(1) 证明: 由折叠的性质, 得 $AD = AD'$, $DE = D'E$, $∠DAE = ∠D'AE$.
∵ 四边形 $ABCD$ 是平行四边形,
∴ $AB = DC$, $AB // DC$,
∴ $∠DEA = ∠EAD'$,
∴ $∠DAE = ∠DEA$,
∴ $AD = AD' = DE = D'E$,
∴ $CE = D'B$,
∴ 四边形 $BCED'$ 是平行四边形.
∵ $AB = 2$, $AD = 1$,
∴ $BC = 1$, $AD' = 1$, 则 $BD' = 1$.
∴ $BC = BD'$,
∴ 四边形 $BCED'$ 是菱形.
(2) 由折叠可知, 点 $D$ 与点 $D'$ 关于 $AE$ 对称. 如图, 连接 $BD$ 交 $AE$ 于点 $P$, 过点 $D$ 作 $DG \perp BA$ 于点 $G$, 则 $BD$ 的长即为 $PD' + PB$ 的最小值.
∵ $CD // AB$,
∴ $∠DAG = ∠CDA = 60^{\circ}$,
∴ $∠ADG = 30^{\circ}$.
∵ $AD = 1$,
∴ $AG = \frac{1}{2}$,
∴ $DG = \frac{\sqrt{3}}{2}$, $BG = \frac{5}{2}$,
∴ $BD = \sqrt{DG^{2} + BG^{2}} = \sqrt{7}$.
故 $PD' + PB$ 的最小值为 $\sqrt{7}$.

解:
(1) 证明: 由折叠的性质, 得 $AD = AD'$, $DE = D'E$, $∠DAE = ∠D'AE$.
∵ 四边形 $ABCD$ 是平行四边形,
∴ $AB = DC$, $AB // DC$,
∴ $∠DEA = ∠EAD'$,
∴ $∠DAE = ∠DEA$,
∴ $AD = AD' = DE = D'E$,
∴ $CE = D'B$,
∴ 四边形 $BCED'$ 是平行四边形.
∵ $AB = 2$, $AD = 1$,
∴ $BC = 1$, $AD' = 1$, 则 $BD' = 1$.
∴ $BC = BD'$,
∴ 四边形 $BCED'$ 是菱形.
(2) 由折叠可知, 点 $D$ 与点 $D'$ 关于 $AE$ 对称. 如图, 连接 $BD$ 交 $AE$ 于点 $P$, 过点 $D$ 作 $DG \perp BA$ 于点 $G$, 则 $BD$ 的长即为 $PD' + PB$ 的最小值.
∵ $CD // AB$,
∴ $∠DAG = ∠CDA = 60^{\circ}$,
∴ $∠ADG = 30^{\circ}$.
∵ $AD = 1$,
∴ $AG = \frac{1}{2}$,
∴ $DG = \frac{\sqrt{3}}{2}$, $BG = \frac{5}{2}$,
∴ $BD = \sqrt{DG^{2} + BG^{2}} = \sqrt{7}$.
故 $PD' + PB$ 的最小值为 $\sqrt{7}$.

9. 如图,在矩形ABCD中,$AB = 8$,$BC = 4$,将矩形沿AC折叠,点D落在点$D'$处,则重叠部分$\triangle AFC$的面积为(
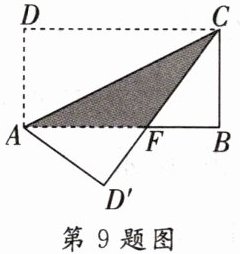
A.6
B.8
C.10
D.12
C
)
A.6
B.8
C.10
D.12
答案:
C
10. 如图,在菱形ABCD中,$\angle ABC = 120^{\circ}$,将菱形折叠,使点A落在对角线BD上的点G处(不与点B,D重合),折痕为EF.若$DG = 2$,$BG = 6$,则$\triangle BEG$的面积为(
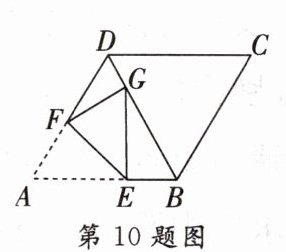
A.$\frac{22\sqrt{3}}{5}$
B.$\frac{21\sqrt{3}}{5}$
C.$4\sqrt{3}$
D.$5\sqrt{3}$
B
)
A.$\frac{22\sqrt{3}}{5}$
B.$\frac{21\sqrt{3}}{5}$
C.$4\sqrt{3}$
D.$5\sqrt{3}$
答案:
B
11. 如下图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
证明:∵ 四边形 $ABCD$ 为矩形,
∴ $AB = CD$, $AD // BC$, $∠D = ∠B = 90^{\circ}$,
∴ $∠FAM = ∠ECM$.
由折叠, 得 $AM = AB$, $CN = CD$, $∠FNC = ∠D = 90^{\circ}$, $∠AME = ∠B = 90^{\circ}$,
∴ $∠ANF = 90^{\circ}$, $∠CME = 90^{\circ}$, $AM = CN$,
∴ $AM - MN = CN - MN$, 即 $AN = CM$.
在 $△ANF$ 和 $△CME$ 中, $\begin{cases} ∠FAN = ∠ECM, \\ AN = CM, \\ ∠ANF = ∠CME, \end{cases}$
∴ $△ANF \cong △CME$(
又 ∵ $AF // CE$, ∴ 四边形 $AECF$ 是平行四边形.
(2)若$AB = 6$,$AC = 10$,求四边形AECF的面积.
∵ $AB = 6$, $AC = 10$, ∴ $BC = \sqrt{AC^{2} - AB^{2}} =$
设 $CE = x$, 则 $EM = BE = 8 - x$.
在 $Rt△CEM$ 中, $(8 - x)^{2} + 4^{2} = x^{2}$, 解得 $x =$
∴ 四边形 $AECF$ 的面积为 $EC \cdot AB = 5 × 6 =$
(1)求证:四边形AECF是平行四边形;
证明:∵ 四边形 $ABCD$ 为矩形,
∴ $AB = CD$, $AD // BC$, $∠D = ∠B = 90^{\circ}$,
∴ $∠FAM = ∠ECM$.
由折叠, 得 $AM = AB$, $CN = CD$, $∠FNC = ∠D = 90^{\circ}$, $∠AME = ∠B = 90^{\circ}$,
∴ $∠ANF = 90^{\circ}$, $∠CME = 90^{\circ}$, $AM = CN$,
∴ $AM - MN = CN - MN$, 即 $AN = CM$.
在 $△ANF$ 和 $△CME$ 中, $\begin{cases} ∠FAN = ∠ECM, \\ AN = CM, \\ ∠ANF = ∠CME, \end{cases}$
∴ $△ANF \cong △CME$(
ASA
), ∴ $AF = CE$.又 ∵ $AF // CE$, ∴ 四边形 $AECF$ 是平行四边形.
(2)若$AB = 6$,$AC = 10$,求四边形AECF的面积.
∵ $AB = 6$, $AC = 10$, ∴ $BC = \sqrt{AC^{2} - AB^{2}} =$
8
, $CM = 10 - 6 =$4
.设 $CE = x$, 则 $EM = BE = 8 - x$.
在 $Rt△CEM$ 中, $(8 - x)^{2} + 4^{2} = x^{2}$, 解得 $x =$
5
,∴ 四边形 $AECF$ 的面积为 $EC \cdot AB = 5 × 6 =$
30
.
答案:
解:
(1) 证明:
∵ 四边形 $ABCD$ 为矩形,
∴ $AB = CD$, $AD // BC$, $∠D = ∠B = 90^{\circ}$,
∴ $∠FAM = ∠ECM$.
由折叠, 得 $AM = AB$, $CN = CD$, $∠FNC = ∠D = 90^{\circ}$, $∠AME = ∠B = 90^{\circ}$,
∴ $∠ANF = 90^{\circ}$, $∠CME = 90^{\circ}$, $AM = CN$,
∴ $AM - MN = CN - MN$, 即 $AN = CM$.
在 $△ANF$ 和 $△CME$ 中, $\begin{cases} ∠FAN = ∠ECM, \\ AN = CM, \\ ∠ANF = ∠CME, \end{cases}$
∴ $△ANF \cong △CME(ASA)$,
∴ $AF = CE$.
又
∵ $AF // CE$,
∴ 四边形 $AECF$ 是平行四边形.
(2)
∵ $AB = 6$, $AC = 10$,
∴ $BC = \sqrt{AC^{2} - AB^{2}} = 8$, $CM = 10 - 6 = 4$.
设 $CE = x$, 则 $EM = BE = 8 - x$.
在 $Rt△CEM$ 中, $(8 - x)^{2} + 4^{2} = x^{2}$, 解得 $x = 5$,
∴ 四边形 $AECF$ 的面积为 $EC \cdot AB = 5 × 6 = 30$.
(1) 证明:
∵ 四边形 $ABCD$ 为矩形,
∴ $AB = CD$, $AD // BC$, $∠D = ∠B = 90^{\circ}$,
∴ $∠FAM = ∠ECM$.
由折叠, 得 $AM = AB$, $CN = CD$, $∠FNC = ∠D = 90^{\circ}$, $∠AME = ∠B = 90^{\circ}$,
∴ $∠ANF = 90^{\circ}$, $∠CME = 90^{\circ}$, $AM = CN$,
∴ $AM - MN = CN - MN$, 即 $AN = CM$.
在 $△ANF$ 和 $△CME$ 中, $\begin{cases} ∠FAN = ∠ECM, \\ AN = CM, \\ ∠ANF = ∠CME, \end{cases}$
∴ $△ANF \cong △CME(ASA)$,
∴ $AF = CE$.
又
∵ $AF // CE$,
∴ 四边形 $AECF$ 是平行四边形.
(2)
∵ $AB = 6$, $AC = 10$,
∴ $BC = \sqrt{AC^{2} - AB^{2}} = 8$, $CM = 10 - 6 = 4$.
设 $CE = x$, 则 $EM = BE = 8 - x$.
在 $Rt△CEM$ 中, $(8 - x)^{2} + 4^{2} = x^{2}$, 解得 $x = 5$,
∴ 四边形 $AECF$ 的面积为 $EC \cdot AB = 5 × 6 = 30$.
12. 在复习菱形的判定和性质时,王老师提出这样一个问题:
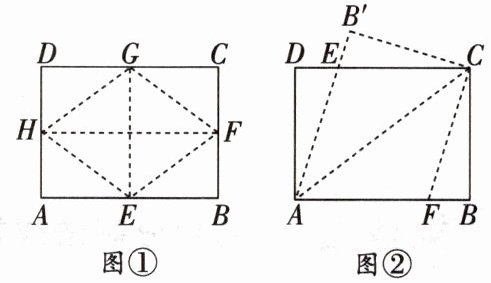
将一个长、宽分别为40 cm和30 cm的矩形ABCD剪成一个菱形并求其面积.
以下是两位同学的想法:
小明的想法是取矩形各边的中点E,F,G,H,连接EF,FG,GH,HE,HF,GE,则四边形EFGH是菱形,如图①,则四边形EFGH的面积是$\frac{1}{2}HF \cdot EG = \frac{1}{2} × 40 × 30 = 600(cm^{2})$;
小刚的想法是沿矩形ABCD的对角线AC折叠,使AB上的点F与DC上的点E重合,展开矩形,连接AE,CF,得到四边形AFCE,如图②.
(1)请证明图②中的四边形AFCE是菱形;
(2)请求出四边形AFCE的面积.
将一个长、宽分别为40 cm和30 cm的矩形ABCD剪成一个菱形并求其面积.
以下是两位同学的想法:
小明的想法是取矩形各边的中点E,F,G,H,连接EF,FG,GH,HE,HF,GE,则四边形EFGH是菱形,如图①,则四边形EFGH的面积是$\frac{1}{2}HF \cdot EG = \frac{1}{2} × 40 × 30 = 600(cm^{2})$;
小刚的想法是沿矩形ABCD的对角线AC折叠,使AB上的点F与DC上的点E重合,展开矩形,连接AE,CF,得到四边形AFCE,如图②.
(1)请证明图②中的四边形AFCE是菱形;
(2)请求出四边形AFCE的面积.

答案:
解:
(1) 证明: 如图, 连接 $EF$, 交 $AC$ 于点 $O$. 由折叠的性质可知, $AE = AF$, $CF = CE$, $∠1 = ∠2$.
∵ 四边形 $ABCD$ 是矩形,
∴ $AB // CD$,
∴ $∠2 = ∠3$,
∴ $∠1 = ∠3$,
∴ $AE = CE$,
∴ $AF = CF = CE = EA$,
∴ 四边形 $AFCE$ 是菱形.
(2)
∵ 四边形 $AFCE$ 是菱形,
∴ $AC$ 与 $EF$ 互相垂直平分.
设 $AF = x \, \text{cm}$, 则 $FB = (40 - x) \, \text{cm}$, $CF = x \, \text{cm}$.
在 $Rt△CFB$ 中, $CF^{2} = BF^{2} + BC^{2}$,
即 $x^{2} = (40 - x)^{2} + 30^{2}$,
解得 $x = \frac{125}{4}$,
∴ $AF = \frac{125}{4} \, \text{cm}$,
∴ 菱形 $AFCE$ 的面积为 $AF \cdot BC = \frac{125}{4} × 30 = \frac{1875}{2} (\text{cm}^{2})$.

解:
(1) 证明: 如图, 连接 $EF$, 交 $AC$ 于点 $O$. 由折叠的性质可知, $AE = AF$, $CF = CE$, $∠1 = ∠2$.
∵ 四边形 $ABCD$ 是矩形,
∴ $AB // CD$,
∴ $∠2 = ∠3$,
∴ $∠1 = ∠3$,
∴ $AE = CE$,
∴ $AF = CF = CE = EA$,
∴ 四边形 $AFCE$ 是菱形.
(2)
∵ 四边形 $AFCE$ 是菱形,
∴ $AC$ 与 $EF$ 互相垂直平分.
设 $AF = x \, \text{cm}$, 则 $FB = (40 - x) \, \text{cm}$, $CF = x \, \text{cm}$.
在 $Rt△CFB$ 中, $CF^{2} = BF^{2} + BC^{2}$,
即 $x^{2} = (40 - x)^{2} + 30^{2}$,
解得 $x = \frac{125}{4}$,
∴ $AF = \frac{125}{4} \, \text{cm}$,
∴ 菱形 $AFCE$ 的面积为 $AF \cdot BC = \frac{125}{4} × 30 = \frac{1875}{2} (\text{cm}^{2})$.

查看更多完整答案,请扫码查看


