2025年魔力暑假A计划八年级数学湘教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年魔力暑假A计划八年级数学湘教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 在$Rt△ABC$中,$∠C= 90^{\circ }$,且$AB= 13$,$BC= 12$,则$AC$等于(
A.11
B.8
C.5
D.3
C
)A.11
B.8
C.5
D.3
答案:
1.C
2. 如图,以$Rt△ABC$的三边为边,分别向外作正方形,它们的面积分别为$S_{1}$,$S_{2}$,$S_{3}$。若$S_{1}= 3$,$S_{2}= 4$,则$S_{3}$的值为(
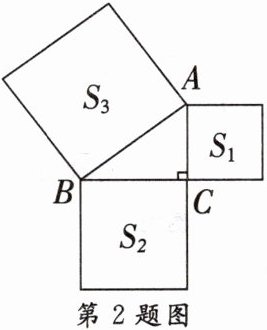
A.5
B.6
C.7
D.8
C
)
A.5
B.6
C.7
D.8
答案:
2.C
3. 如图,在$3×3$的网格中,每个小正方形的边长均为 1,点$A$,$B$,$C$都在格点上。若$BD$为$△ABC$的高,则$BD$的长为(
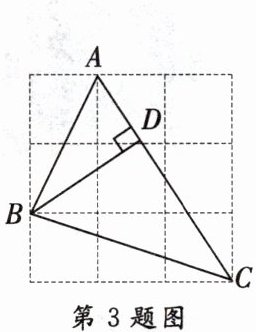
A.$\frac {10}{13}\sqrt {13}$
B.$\frac {9}{13}\sqrt {13}$
C.$\frac {8}{13}\sqrt {13}$
D.$\frac {7}{13}\sqrt {13}$
D
)
A.$\frac {10}{13}\sqrt {13}$
B.$\frac {9}{13}\sqrt {13}$
C.$\frac {8}{13}\sqrt {13}$
D.$\frac {7}{13}\sqrt {13}$
答案:
3.D
4. 如图,在四边形$ABCD$中,$∠D= ∠ACB= 90^{\circ }$,$CD= 12$,$AD= 16$,$BC= 15$,则$AB= $(

A.20
B.25
C.35
D.30
B
)
A.20
B.25
C.35
D.30
答案:
4.B
5. (包头中考)如图,在$Rt△ABC$中,$∠ACB= 90^{\circ }$,$D是AB$的中点,$BE⊥CD$,交$CD的延长线于点E$。若$AC= 2$,$BC= 2\sqrt {2}$,则$BE$的长为(

A.$\frac {2\sqrt {6}}{3}$
B.$\frac {\sqrt {6}}{2}$
C.$\sqrt {3}$
D.$\sqrt {2}$
A
)
A.$\frac {2\sqrt {6}}{3}$
B.$\frac {\sqrt {6}}{2}$
C.$\sqrt {3}$
D.$\sqrt {2}$
答案:
5.A [解析]
∵在Rt△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{2}$,
∴由勾股定理,得$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{2^{2} + (2\sqrt{2})^{2}} = 2\sqrt{3}$。
∵D是AB的中点,
∴$BD = CD = \frac{1}{2}AB = \sqrt{3}$。
设$DE = x$,则$CE = \sqrt{3} + x$。
由勾股定理,得$(\sqrt{3})^{2} - x^{2} = (2\sqrt{2})^{2} - (\sqrt{3} + x)^{2}$,
解得$x = \frac{\sqrt{3}}{3}$。
∴在Rt△BED中,$BE = \sqrt{BD^{2} - DE^{2}} = \sqrt{(\sqrt{3})^{2} - (\frac{\sqrt{3}}{3})^{2}} = \frac{2\sqrt{6}}{3}$。
∵在Rt△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{2}$,
∴由勾股定理,得$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{2^{2} + (2\sqrt{2})^{2}} = 2\sqrt{3}$。
∵D是AB的中点,
∴$BD = CD = \frac{1}{2}AB = \sqrt{3}$。
设$DE = x$,则$CE = \sqrt{3} + x$。
由勾股定理,得$(\sqrt{3})^{2} - x^{2} = (2\sqrt{2})^{2} - (\sqrt{3} + x)^{2}$,
解得$x = \frac{\sqrt{3}}{3}$。
∴在Rt△BED中,$BE = \sqrt{BD^{2} - DE^{2}} = \sqrt{(\sqrt{3})^{2} - (\frac{\sqrt{3}}{3})^{2}} = \frac{2\sqrt{6}}{3}$。
6. 如图所示,阴影部分是一个等腰直角三角形,则此等腰直角三角形的面积为____。

6. 如图所示,阴影部分是一个等腰直角三角形,则此等腰直角三角形的面积为


6. 如图所示,阴影部分是一个等腰直角三角形,则此等腰直角三角形的面积为
40.5
。
答案:
6.40.5
7. 在$Rt△ABC$中,$∠C= 90^{\circ }$。若$AB-AC= 2$,$BC= 8$,则$AB$的长是____
17
。
答案:
7.17
8. 如图,边长为 2 的等边三角形$ABC的两个顶点A$,$B分别在两条射线OM$,$ON$上滑动。若$OM⊥ON$,则$OC$的最大值是____。


答案:
8.1+$\sqrt{3}$ [解析]如图,取AB的中点D,连接OD,DC.
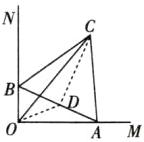
∵OC≤OD+DC,
∴当O,D,C三点共线时,OC有最大值,最大值是OD+CD。
∵△ABC为等边三角形,D为AB的中点,
∴BD=1,BC=2,CD⊥AB,
∴$CD = \sqrt{BC^{2} - BD^{2}} = \sqrt{3}$。
∵OM⊥ON,D为AB的中点,
∴在Rt△AOB中,$OD = \frac{1}{2}AB = 1$。
∴$OD + CD = 1 + \sqrt{3}$,即OC的最大值为$1 + \sqrt{3}$。
8.1+$\sqrt{3}$ [解析]如图,取AB的中点D,连接OD,DC.

∵OC≤OD+DC,
∴当O,D,C三点共线时,OC有最大值,最大值是OD+CD。
∵△ABC为等边三角形,D为AB的中点,
∴BD=1,BC=2,CD⊥AB,
∴$CD = \sqrt{BC^{2} - BD^{2}} = \sqrt{3}$。
∵OM⊥ON,D为AB的中点,
∴在Rt△AOB中,$OD = \frac{1}{2}AB = 1$。
∴$OD + CD = 1 + \sqrt{3}$,即OC的最大值为$1 + \sqrt{3}$。
9. (苏州期中)如下图,在$Rt△ABC$中,$∠ACB= 90^{\circ }$,$AC= 20$,$BC= 15$,$CD⊥AB于点D$。求:
(1)$CD$的长:
∵在$Rt△ABC$中,$∠ACB = 90^{\circ }$,$BC = 15$,$AC = 20$,
∴由勾股定理,得$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{20^{2} + 15^{2}} = 25$。
∵$S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD$,
∴$AC \cdot BC = AB \cdot CD$,
∴$CD = \frac{AC \cdot BC}{AB} = \frac{20 × 15}{25} =$
∴$CD$的长是
(2)$BD$的长:
∵$CD⊥AB$于点$D$,
∴$∠CDB = 90^{\circ }$。
∵在$Rt△BCD$中,$∠CDB = 90^{\circ }$,$BC = 15$,$CD = 12$,
∴由勾股定理,得$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{15^{2} - 12^{2}} =$
∴$BD$的长是

(1)$CD$的长:
∵在$Rt△ABC$中,$∠ACB = 90^{\circ }$,$BC = 15$,$AC = 20$,
∴由勾股定理,得$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{20^{2} + 15^{2}} = 25$。
∵$S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD$,
∴$AC \cdot BC = AB \cdot CD$,
∴$CD = \frac{AC \cdot BC}{AB} = \frac{20 × 15}{25} =$
12
,∴$CD$的长是
12
。(2)$BD$的长:
∵$CD⊥AB$于点$D$,
∴$∠CDB = 90^{\circ }$。
∵在$Rt△BCD$中,$∠CDB = 90^{\circ }$,$BC = 15$,$CD = 12$,
∴由勾股定理,得$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{15^{2} - 12^{2}} =$
9
,∴$BD$的长是
9
。
答案:
9.解:
(1)
∵在Rt△ABC中,∠ACB=90°,BC=15,AC =20,
∴由勾股定理,得$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{20^{2} + 15^{2}} = 25$。
∵$S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD$,
∴$AC \cdot BC = AB \cdot CD$,
∴$CD = \frac{AC \cdot BC}{AB} = \frac{20 × 15}{25} = 12$,
∴CD的长是12。
(2)
∵CD⊥AB于点D,
∴∠CDB=90°。
∵在Rt△BCD中,∠CDB=90°,BC=15,CD=12,
∴由勾股定理,得$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{15^{2} - 12^{2}} = 9$,
∴BD的长是9。
(1)
∵在Rt△ABC中,∠ACB=90°,BC=15,AC =20,
∴由勾股定理,得$AB = \sqrt{AC^{2} + BC^{2}} = \sqrt{20^{2} + 15^{2}} = 25$。
∵$S_{\triangle ABC} = \frac{1}{2}AC \cdot BC = \frac{1}{2}AB \cdot CD$,
∴$AC \cdot BC = AB \cdot CD$,
∴$CD = \frac{AC \cdot BC}{AB} = \frac{20 × 15}{25} = 12$,
∴CD的长是12。
(2)
∵CD⊥AB于点D,
∴∠CDB=90°。
∵在Rt△BCD中,∠CDB=90°,BC=15,CD=12,
∴由勾股定理,得$BD = \sqrt{BC^{2} - CD^{2}} = \sqrt{15^{2} - 12^{2}} = 9$,
∴BD的长是9。
查看更多完整答案,请扫码查看


